神秘的二進位計算
前幾天遇到一個考題,題目內容是:「使用者輸入二個十進位數字,在二進位的表示下,要調整幾個位元才能讓二個數字相等?」
例:
「211 = 1101 0011」
「90 = 0101 1010」
這二個數字套到上面題目時,答案應該要是「3」。因為要修改 3 個位元後,二個數字才會相等。
一開始的解法很單純。把二個數字轉位二進位的字串,然後迴圈逐字比對。
static void ProcessByString(int value1, int value2)
{
string x = Convert.ToString(value1, 2);
string y = Convert.ToString(value2, 2);
int nMax = x.Length > y.Length ? x.Length : y.Length;
x=x.PadLeft(nMax, '0');
y=y.PadLeft(nMax, '0');
int nResult = 0;
for (int i = 0; i < nMax; i++)
{
nResult += x[i] == y[i] ? 0 : 1;
}
}
這個解法,是相當直接也簡單的。但雖然在邏輯上正確,在「效能」上卻大打折扣。
底下是後來再想的解法。
static void ProcessByBinary(int value1, int value2)
{
int x = value1 ^ value2;
int nResult = 0;
while (x!= 0)
{
nResult++;
x &= x - 1;
}
}
這樣的解法是先用 xor 作二位元的計算,計算後即可知道各位元有哪些不同。
然後再用 & 運算元來圈計算總數是多少。
用一段跑一仟萬次的迴圈來測試二段的效能差異。
var watch = new Stopwatch();
watch.Start();
for (int i = 0; i < 10000000; i++)
{
ProcessByString(i, i+88);
//ProcessByBinary(i, i + 88);
}
watch.Stop();
Console.WriteLine($"consumed time:{watch.ElapsedMilliseconds}");
Console.ReadLine();
首先,是第一種解法所跑出來的時間(毫秒)。
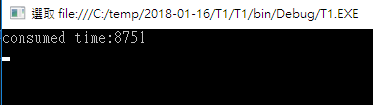
再來,是第二種解法所跑出來的時間(毫秒)。
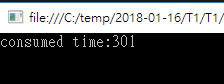
天啊,二者的差距差到 20 倍以上。真懷疑我的第一個解法是怎麼想出來的。
這樣的程式在一般小型系統可能沒什麼問題,到了真的大流量的系統上,這應該很快就噴了……
心得:要往更高一層的程式設計 level,在思考問題時,實在不能以直接的邏輯來推,而是要以電腦運算的邏輯來推,才是較正確的作法。
參考連結: