阿夢的程式設計天地

氣泡排序演算法的運作原理如下:

1.比較相鄰的元素，如果第一個元素比第二個元素大(小)，就交換這兩個元素。

2.對每一對相鄰的元素執行同樣的行為，從開始的第一對到結尾的最後一對。當這部做完之後最後的元素會是最大(小)的數。

3.針對除了最後一個已經排序過後的數之外重複步驟一跟步驟二。

4.持續每次對越來越少的未排序的元素重複上面的步驟，直到沒有任何一對數字需要比較。

執行時，未排序資料中的最大值會如同氣泡般往右邊移動，故此命名為氣泡排序法。

範例: 由小到大排序 3 7 1 2 9 4
第一輪:
3 7 1 2 9 4 
3 7 1 2 9 4
3 1 7 2 9 4 
3 1 2 7 9 4
3 1 2 7 9 4
3 1 2 7 4 9  (此時9是最大的已排序的數，故第二輪無須交換他)
第二輪:
3 1 2 7 4 9
1 3 2 7 4 9
1 2 3 7 4 9
1 2 3 7 4 9
1 2 3 4 7 9 (此時7是第二大的已排序的數，故第三輪無須交換他)
第三輪:
1 2 3 4 7 9 (此時4是第三大的已排序的數，故第四輪無須交換他)
第四輪:
1 2 3 4 7 9 (此時3是第四大的已排序的數，故第五輪無須交換他)
第五輪:
1 2 3 4 7 9 (此時2是第五大的已排序的數，故第六輪無須交換他)
第六輪:
1 2 3 4 7 9 (此時1是第六大的已排序的數，且也已經沒有未排序的數，由此可知1 2 3 4 7 9是最終由小到大排序)

時間複雜度如下:

最佳時間複雜度：O(n):當資料的順序恰好是所選擇的排序方式時。

平均時間複雜度：O(n^2):第n筆資料，平均比較(n-1)/2 次。

最差時間複雜度：O(n^2):當資料的排序恰好是所選擇的相反排序方式時。

其原理的虛擬碼大致如下:

template < typename T > //整數或浮點數皆可使用

void bubbleSort (T arr[], int len){
    int i, j, temp;
    for( i = to len-2)
    {
     for(j = 0 to length-2-i)
     {
       if(array[j]>array[j+1])
          temp = arr[j];
          arr[j] = arr[j + 1];
          arr[j + 1] = temp;
     }
    }
}

完整程式碼如下: 

#include <iostream>
using namespace std;

int bubbleSort(int[], int);


int main()
{

	int *ptr;//宣告指標ptr
	int size;//宣告陣列大小

	cout << "請輸入陣列大小:";
	cin >> size;//輸入陣列大小

	ptr = new int[size];//建立動態記憶體陣列

	for (int i = 0; i < size; i++)
	{
		cin >> *(ptr + i);//輸入陣列中的資料
	}

	cout << "排序前:" << endl;

	for (int j = 0; j < size; j++)
	{
		cout << *(ptr + j) << " ";//印出陣列中的資料
	}

	cout << endl;

	bubbleSort(ptr, size);

	cout << "排序後:" << endl;

	for (int k = 0; k < size; k++)
	{
		cout << *(ptr + k) << " ";//印出排序後的陣列中的資料
	}
	system("pause");
	return 0;
}

int bubbleSort(int a[], int len)
{
	int i, j, temp;
	for (i = 0; i < len - 1; i++)
		for (j = 0; j < len - 1 - i; j++)
			if (a[j] > a[j + 1]) 
                temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
	return *a;
}

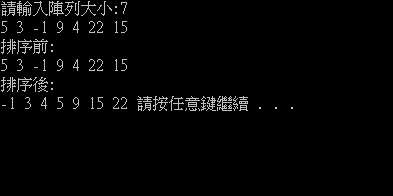
執行結果如下:

有夢最美 築夢踏實

活在當下 認真過每一天

我是阿夢 也是Ace