四月的筆記

第一集在這裡喔:https://dotblogs.com.tw/April_Notes/2021/12/08/113301

這個範例為:
ax1  +  bx2  + cx3  + dx4  =  30
ax5  +  bx6  + cx7  + dx8  =  70
ax9  +  bx10 + cx11 + dx12 = 110
ax13 +  bx14 + cx15 + dx16 = 150
ax17 +  bx18 + cx19 + dx20 = 190

求解: a、b、c、d  

由這樣設定上可以看到:

簡單來說設定上就是:

方程式: f(X1,X2,X3,X4) = aX1 + bX2 + cX3 + dX4 = Y

Xij =  
1	2	3	4
5	6	7	8
9	10	11	12
13	14	15	16
17	18	19	20

Yi =
30
70
110
150
190

這個題目用矩陣就有解，但是我們用Fitting方式來完成

Fitting的程式代碼為:

#include <cstdio>
#include <vector>
#include "lmmin.h"
#include <iostream>
#include <string>
#include <fstream>



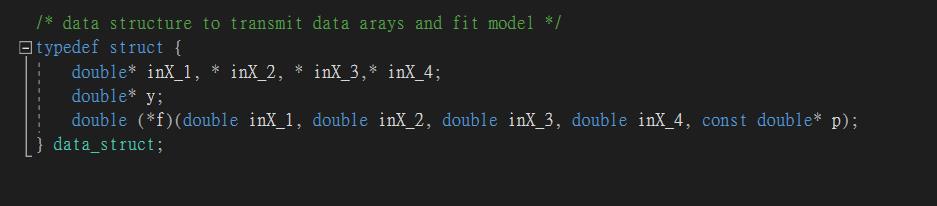
/* data structure to transmit data arays and fit model */
typedef struct {
    double* inX_1, * inX_2, * inX_3,* inX_4;
    double* y;
    double (*f)(double inX_1, double inX_2, double inX_3, double inX_4, const double* p);
} data_struct;




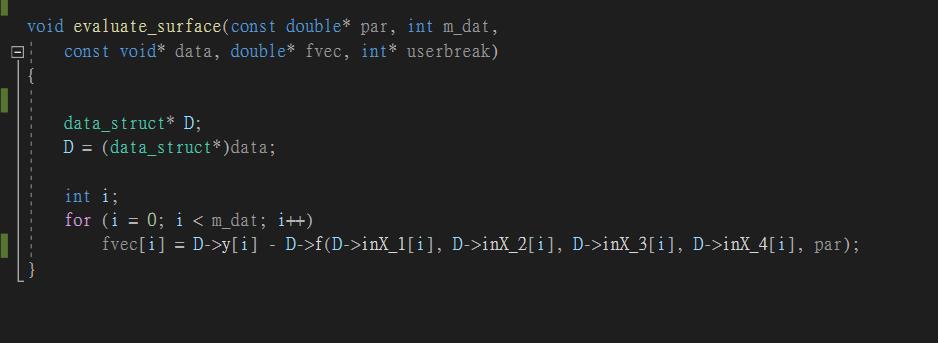
void evaluate_surface(const double* par, int m_dat,
    const void* data, double* fvec, int* userbreak)
{
    
    data_struct* D;
    D = (data_struct*)data;

    int i;
    for (i = 0; i < m_dat; i++)
        fvec[i] = D->y[i] - D->f(D->inX_1[i], D->inX_2[i], D->inX_3[i], D->inX_4[i], par);
}




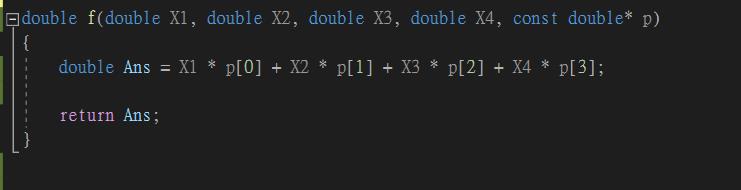
double f(double X1, double X2, double X3, double X4, const double* p)
{
    double Ans = X1 * p[0] + X2 * p[1] + X3 * p[2] + X4 * p[3];
   
    return Ans;
}





const int Num_par = 4;
const int Num_dat = 5;


void Fitting_function(
    std::vector<double>& par_Vector,
    const std::vector<std::vector<double>>& X_dat,
    const std::vector<double>& Y_dat)
{

    /* parameter vector */
    int n_par = Num_par;/* number of parameters in model function f */
    double par[Num_par];/* arbitrary starting value */

    for (int i = 0; i < Num_par; i++)
        par[i] = par_Vector[i];


    /* data points */
    int m_dat = Num_dat;
    double inX_1[Num_dat], inX_2[Num_dat], inX_3[Num_dat], inX_4[Num_dat], y[Num_dat];



    for (int i = 0; i < Num_dat; i++)
    {
        inX_1[i] = X_dat[i][0];
        inX_2[i] = X_dat[i][1];
        inX_3[i] = X_dat[i][2];
        inX_4[i] = X_dat[i][3];
    }



    for (int i = 0; i < Num_dat; i++)
        y[i] = Y_dat[i];


    data_struct data = { inX_1, inX_2, inX_3,inX_4, y, f };

    /* auxiliary parameters */
    lm_status_struct status;
    lm_control_struct control = lm_control_double;
    control.verbosity = 0;

    /* perform the fit */
    lmmin(n_par, par, m_dat, (const void*)&data, evaluate_surface, &control, &status);

    for (int i = 0; i < n_par; ++i)
        par_Vector[i] = par[i];





}



int main()
{

    //// Initial Value
    std::vector<double> par_Vector;

    par_Vector.push_back(2);
    par_Vector.push_back(2);
    par_Vector.push_back(2);
    par_Vector.push_back(2);


    //// X Data vector 
    std::vector<std::vector<double>> X_dat;
    std::vector<double> YdV;
    std::vector<double> XdV;

    XdV = { 1	,2	,3	,4 };
    X_dat.push_back(XdV);
    YdV.push_back(30);

    XdV = { 5	,6	,7	,8 };
    X_dat.push_back(XdV);
    YdV.push_back(70);

    XdV = { 9	,10	,11	,12 };
    X_dat.push_back(XdV);
    YdV.push_back(110);

    XdV = { 13	,14	,15	,16 };
    X_dat.push_back(XdV);
    YdV.push_back(150);

    XdV = { 17	,18	,19	,20 };
    X_dat.push_back(XdV);
    YdV.push_back(190);


    
    
    std::cout << "Check" << std::endl;
    std::cout << "Num_dat: " << Num_dat << "\t" << X_dat.size() << std::endl;
    std::cout << "Num_par: " << Num_par << "\t" << par_Vector.size() << std::endl;


    
     Fitting_function(par_Vector, X_dat, YdV);

    
    std::cout << "The Fitting Result :" << std::endl;
    std::cout << "X1:\t" << par_Vector[0] << std::endl;
    std::cout << "X2:\t" << par_Vector[1] << std::endl;
    std::cout << "X3:\t" << par_Vector[2] << std::endl;
    std::cout << "X4:\t" << par_Vector[3] << std::endl << std::endl;;
    
    std::cin.get();

    return 0;
}

 

簡單解釋一下:

1. 設定方程式為: f(X1,X2,X3,X4) = aX1 + bX2 + cX3 + dX4 = Y

 

 

 

 

 

 

 

 

 

 

 

2. 判斷的標準為: Y - f(X1,X2,X3,X4) 的最小值 

 

3. 將X 與 Y 數值寫進去
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3. 執行Fitting

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

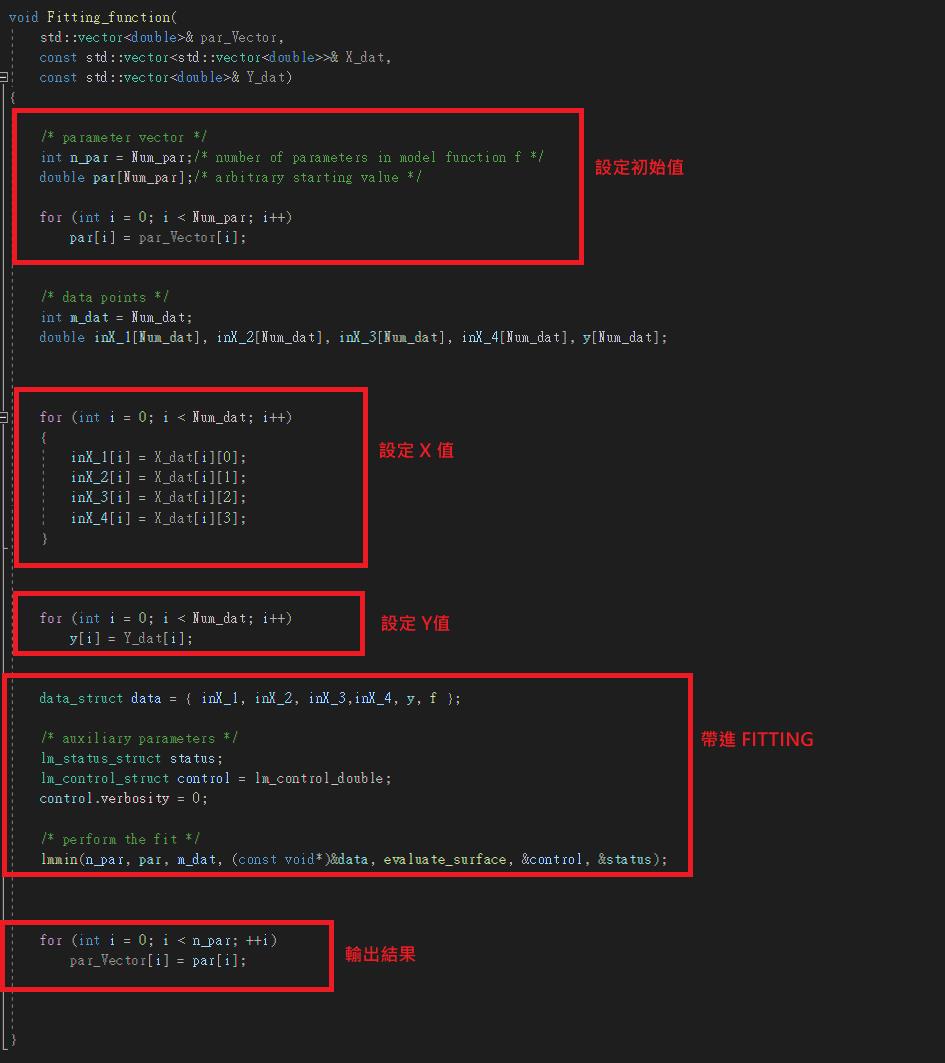
來側看看

 

 

 

 

 

 

 

 

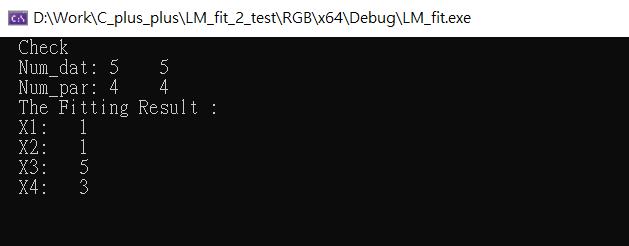
跟預計的結果相同