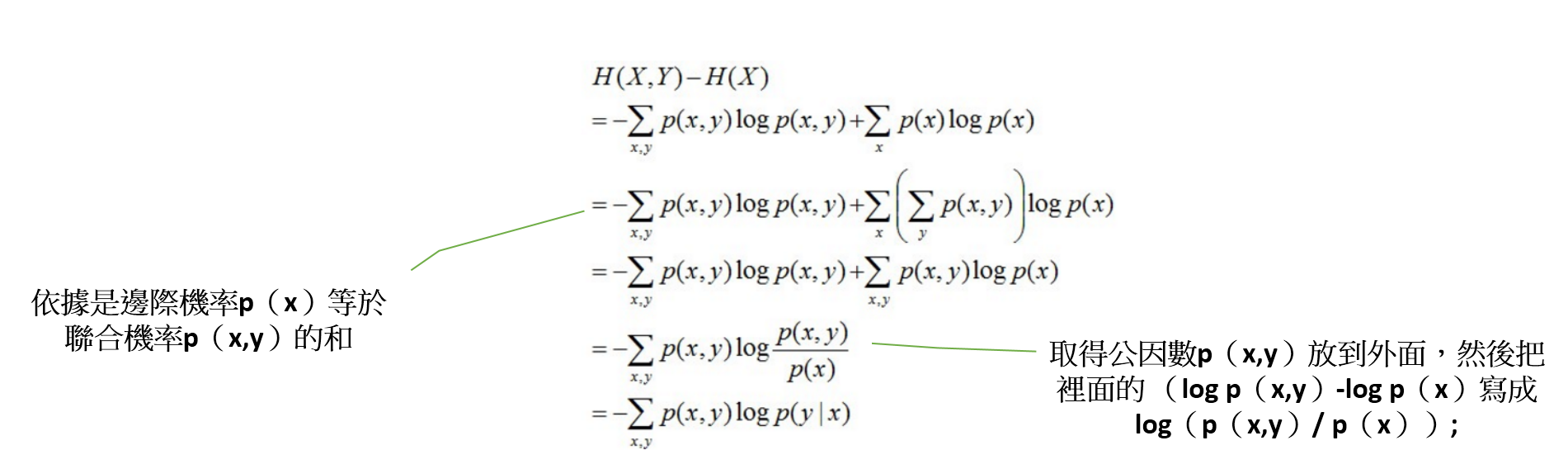Data is anything but not everything

#資訊量

在介紹此模型之前，先跟大家導入資訊量之觀念，這跟最大熵模型非常相關

1. 當事件越明確時，關於此事件所獲得訊息量越小。

   • 例如:太陽從東邊升起(這是既定的事件，完全無法獲得資訊量)

2. 當事件越模糊時，提供一件可供判斷的事情就會含有較多的訊息。

   • 例如:走路跌倒(此事件發生原因有多種可能性，可獲得資訊量相對多)

*所以說資訊量與事件的不確定性有相關 

那不確定性的變化跟什麼有關呢？

1. 跟事情的可能結果的數量有關。
   • 我們討論太陽從哪升起。本來就只有一個結果，那麼無論誰傳遞任何資訊都是沒有資訊量的。
   • 當有多種結果時，我們才會得到較大資訊量。
2. 跟機率有關。
   • 單看結果數量還不夠，還要看初始的機率分佈。
   • 例如:小明在一個有40個座位的電影院看電影。小明可以坐的位置數量算多了。可是假如一開始就知道小明坐在第一排的最左邊的可能是99％，坐在其位置的可能性微乎其微，那麼在大多數情況下，你再告訴我其他資訊也沒有多用處，因為我們幾乎確定小明坐第一排的最左邊了。

 #熵

介紹完資訊量，想必會覺得是個很抽象的概念。我們常常說資訊很多，或者資訊較少，但卻很難說清楚資訊到底有多少。

直到1948 年， Claude Shannon 提出了information theory (then known as communication theory) 的概念後，才解決了對資訊的量化度量問題。

資訊量化公式:i(x)=-log(p(x)) 

畫成圖形如下圖: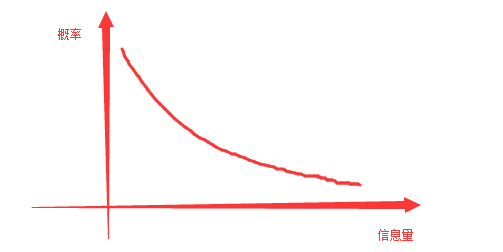

大家可能看到公式就反感，我這邊用簡單的概念來解說這個定義公式

1. 資訊量為正值
   • 別看前面有個負號，把負號挪到log裡面，且機率是介於0~1之間，所以恆為正值。
2. 資訊量可以相加
   • 如果兩個事件X和Y獨立，即p(xy)= p(x)p(y)，假定x和y的資訊量分別為i(x)和i(y)，則二者同時發生的資訊量應該為i(x^y)= i(x)+ i(y) ​​
3. 資訊量與機率相關(上面有提到)
   • 若P(x)= 1，則i(x)= 0。必然事件並不能提供任何資訊量，因為他是必然發生的。
     若P(x)= 0，則i(x) =>∞。如果一個不可能事件發生了，他能提供的資訊量一定非常大且趨近於無窮。

熵就是平均而言發生一個事件我們得到的訊息量大小。所以數學上，熵其實是資訊量的期望(簡單來說就是取得資訊量期望值)

熵公式定義如下:

如果一個隨機變數為X ={X1，X2，...，Xk}，其機率分佈為P（X =xi）= Pi（i =1,2，...，K），則隨機變數X的熵定義為：

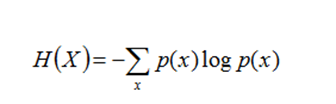
 #熵的相關性

這邊如果沒有統計基礎可能會看得比較辛苦，所以稍微點到即可

1. 聯合熵
   • ​
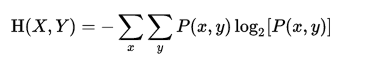
2. 條件熵(最常用的定義式子)
   • H(Y|X)=H(X,Y)–H(X)
   • 推導過程如下
     • 

 #最大熵模型

最大熵模型的本質，它要解決的問題就是已知X，計算Y的概率，且盡可能讓Y的概率最大

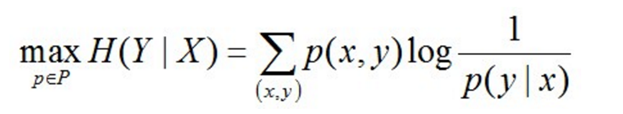
其中，P = {p | p是X上滿足條件的概率分佈}

繼續闡述之前，必須定義特徵函數(所謂的特徵函數就是描述X與Y)。

這裡特徵函數我就直接用論文中的例子來說明

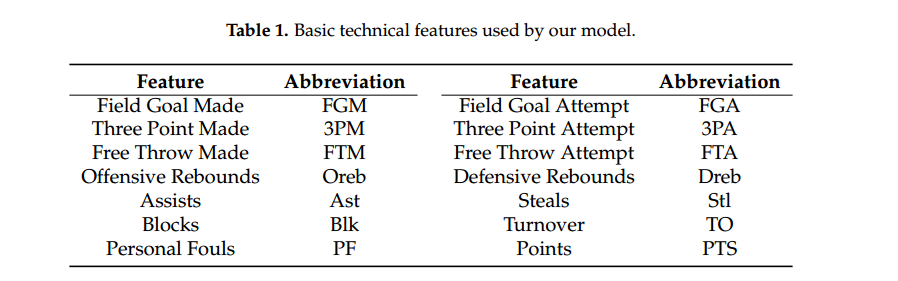每一場比賽每隊有14個變數，因此一場比賽共有28個變數(主隊+客隊)

為了模型表示方便，我們將條件x與結果y表示為二項的函式，稱之特徵函數(Feature Function，如下圖式子)

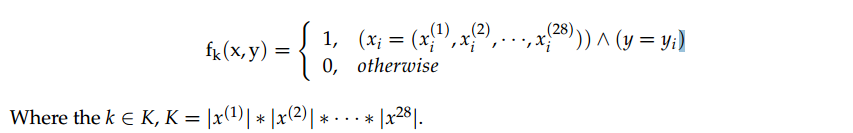
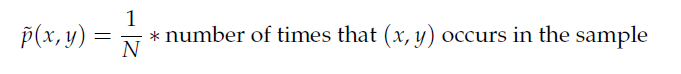
其中的經驗分布(~p)來替帶我們原式子中的p分布，因此函式在樣本中之期望值如下: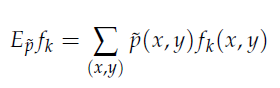由於p(x,y)=p(x)p(y|x)因此推倒如下圖公式，~p(x)一樣式樣本中x的經驗分布

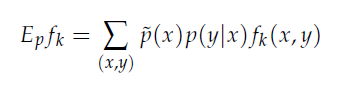
而最大熵模模型就是在特徵函數限制下選擇最優的機率分佈，如下圖

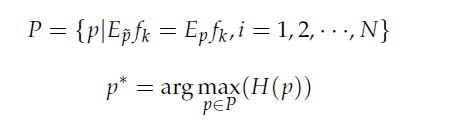而這邊就是要去解最佳化的式子，需引入拉格朗乘數(這邊就不推倒，有興趣可自行上網查詢)

#實作

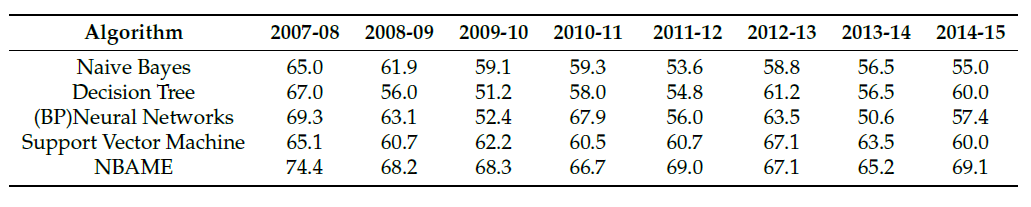上圖為作者實作成果，看命中率個人覺得還行(這邊都是預測勝負)，不過季後賽場次少，如果準確度沒有到七成基本上獲利不會太多

我利用此模型套入(自行搜尋:R maxent)，變數84個，實際去測試後準確度有不錯的表現(2016-2017/2月，NBA比賽)

勝負盤73%，讓分盤63%，大小盤61%，比較舊模型準確度有提升不少

或許在預測資料上面改用權重計算會有更好的成果!!!