相信有在玩資料的各位,迴歸分析並不陌生吧,在「解釋」、「篩選變數」、「預測」中都扮演著舉足輕重的地位。本篇針對Lasso Regression & Ridge Regression做個簡單介紹。
一、Lasso
Lasso由加拿大統計學家Robert Tibshirani所提出,為正規化(regularization)迴歸方法的一種。
1. Lasso特點:可同時進行變數篩選與複雜度調整(正規化) ,何謂正規化呢 ? 其實不用想這麼複雜,它其實只是為了要避免overfitting一種方式。
2. Lasso是在最小平方和中對模型加上正規化(regularizer)或是稱作懲罰項 (penalty term),我們通常稱Lasso懲罰項為L1 norm。
下圖為Lasso公式,也是在解此式子的最佳解,其中lambda為事先給定常數,通常我們會透過交叉驗證 (cross validation) 的方法來決定lambda值 。
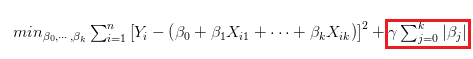
而LASSO的L1 norm的效果可以強制使得不重要的解釋變數 ,其估計出的係數為0 ,因此也達到了變數篩選的功能,
當特徵減少,用來預測的準確度就可以比較穩定,而解釋上也比較容易,也呼應了上面說得避免過適。
二、Ridge
Ridge則是Andrey Tikhonov提出,為正規化(regularization)迴歸方法的一種。
1. Ridge特點:可處理多元共線性問題,但它並不能使估計出的係數為0,所以無法做變數篩選。其道理很好了解,以直觀來看因為它懲罰項是平方,因此它只能趨近於0,但無法等於0。
2. Ridge是在最小平方和中對模型加上正規化(regularizer)或是稱作懲罰項 (penalty term),我們通常稱Lasso懲罰項為L2 norm。
而兩個就是僅差別在於正規項更改而已,如下圖
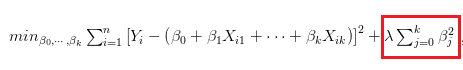
以最佳化的概念來看:
-
Lasso的懲罰項 代表權重的絕對值和給限制,故會形成菱形的可行解域。
-
Ridge的懲罰項 代表權重的平方和給限制,故會形成圓形的可行解域。
所以我們常看到的下圖結構就是這樣來的
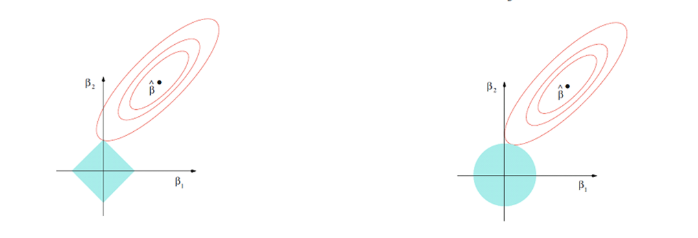
整理一下Lasso特點:
-
除常數項以外,這種回歸的假設與最小二乘回歸類似。
-
由於它收縮系數接近零(等於零),有助於變數選擇(Feature Selection)。
-
為正則化方法,使用的是L1正則化,可避免過度配適。
-
適合特徵為高維稀疏。
整理一下Ridge特點:
-
除常數項以外,這種回歸的假設與最小二乘回歸類似。
-
加入L2 norm,避免模型複雜度太高。
-
為正則化方法,使用的是L2正則化,可避免過度配適。
-
適合特徵為低維稠密。