Brooke

一、題目

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

 

Example 1:

 

 

 

 

 

 

 

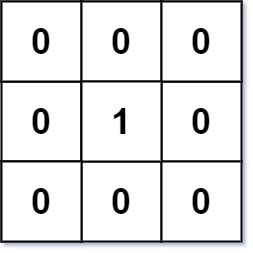
Input: mat = [[0,0,0],[0,1,0],[0,0,0]] Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

 

 

 

 

 

 

 

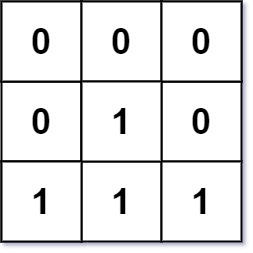
Input: mat = [[0,0,0],[0,1,0],[1,1,1]] Output: [[0,0,0],[0,1,0],[1,2,1]]

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• There is at least one 0 in mat.

 

二、程式作法

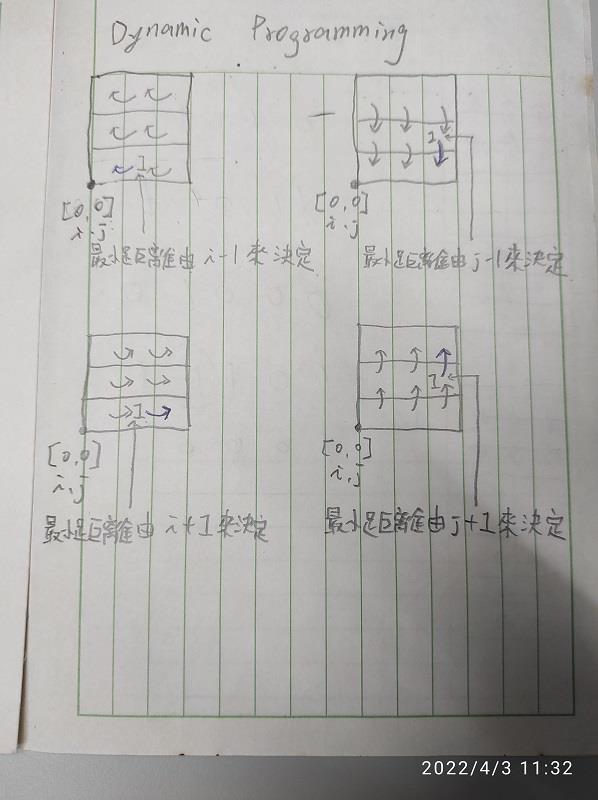
 /*Dynamic Programming*/
public class Solution
{
    public int[][] UpdateMatrix(int[][] mat)
    {
        int[][] dist = new int[mat.Length][];
        for (int i = 0; i < mat.Length; i++)
            dist[i] = new int[mat[0].Length];

        for (int i = 0; i < dist.Length; i++)
            for (int j = 0; j < dist[0].Length; j++)
                dist[i][j] = 10000;

        for (int i = 0; i < mat.Length; i++)
            for (int j = 0; j < mat[0].Length; j++)
                if (mat[i][j] == 0)
                    dist[i][j] = 0;
                else
                {
                    if (i > 0)
                        dist[i][j] = Math.Min(dist[i][j], dist[i - 1][j] + 1);
                    if (j > 0)
                        dist[i][j] = Math.Min(dist[i][j], dist[i][j - 1] + 1);
                }

        for (int i = mat.Length - 1; i >= 0; i--)
            for (int j = mat[0].Length - 1; j >= 0; j--)
                if (mat[i][j] == 0)
                    dist[i][j] = 0;
                else
                {
                    if (i < mat.Length - 1)
                        dist[i][j] = Math.Min(dist[i][j], dist[i + 1][j] + 1);
                    if (j < mat[0].Length - 1)
                        dist[i][j] = Math.Min(dist[i][j], dist[i][j + 1] + 1);
                }

        return dist;
    }
}

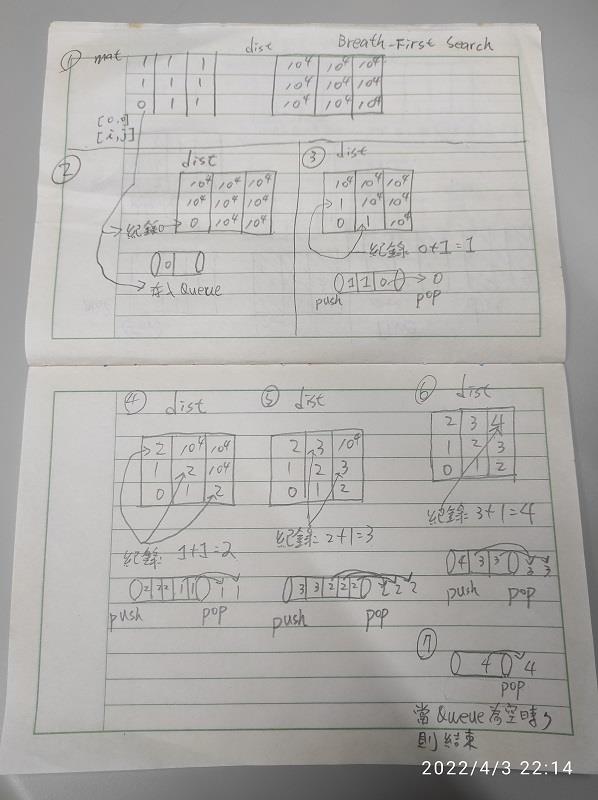
/*Breath-First Search (Time Limit Exceeded)*/
/*
public class Solution
{
    public int[][] UpdateMatrix(int[][] mat)
    {
        int[][] dist = new int[mat.Length][];
        for (int i = 0; i < mat.Length; i++)
            dist[i] = new int[mat[0].Length];

        for (int i = 0; i < dist.Length; i++)
            for (int j = 0; j < dist[0].Length; j++)
                dist[i][j] = 10000;

        Queue<Tuple<int, int>> q = new Queue<Tuple<int, int>>();

        Tuple<int, int>[] dir = new Tuple<int, int>[] {
            new Tuple<int, int>(1, 0),
            new Tuple<int, int>(0, -1),
            new Tuple<int, int>(-1, 0),
            new Tuple<int, int>(0, 1)
        };

        for (int i = 0; i < mat.Length; i++)
            for (int j = 0; j < mat[0].Length; j++)
                if (mat[i][j] == 0)
                {
                    dist[i][j] = 0;
                    q.Enqueue(new Tuple<int, int>(i, j));
                }

        while (q.Count > 0)
        {
            Tuple<int, int> c = q.Dequeue();

            for (int k = 0; k < 4; k++)
                if (dir[k].Item1 + c.Item1 >= 0 &&
                    dir[k].Item1 + c.Item1 <= dist.Length - 1 &&
                    dir[k].Item2 + c.Item2 >= 0 &&
                    dir[k].Item2 + c.Item2 <= dist[0].Length - 1)
                {
                    if (dist[dir[k].Item1 + c.Item1][dir[k].Item2 + c.Item2] > dist[c.Item1][c.Item2] + 1)
                    {
                        dist[dir[k].Item1 + c.Item1][dir[k].Item2 + c.Item2] = dist[c.Item1][c.Item2] + 1;
                        if (!q.Contains(new Tuple<int, int>(dir[k].Item1 + c.Item1, dir[k].Item2 + c.Item2)))
                            q.Enqueue(new Tuple<int, int>(dir[k].Item1 + c.Item1, dir[k].Item2 + c.Item2));
                    }
                }
        }

        return dist;
    }
}
*/

 

三、思路筆記

目的為針對矩陣內的每一個元素，計算其到零的最小距離。

計算一個點到零的最短距離可以根據其上下左右點所回傳的距離得到，

一開始我想可以用 Dynamic Programming 方式以遞迴來處理，

或許思想考方向OK，但實際思路卻卡在想用「遞迴」實作太久，想到最後腦袋直接放空…

看了一些別人的解法後，隔天我各實作兩種解法。

解法一，Dynamic Programming

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

解法二，Breath-First Search (Time Limit Exceeded)