Brooke

一、題目

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

 

Example 1:

Input: nums = [1,2,3] Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

Example 2:

Input: nums = [0,1] Output: [[0,1],[1,0]]

Example 3:

Input: nums = [1] Output: [[1]]

 

Constraints:

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• All the integers of nums are unique.

 

二、程式作法

/*use list index*/
public class Solution
{
    public IList<IList<int>> result = new List<IList<int>>();
    public int[] nums = Array.Empty<int>();
    public IList<IList<int>> Permute(int[] nums)
    {
        this.nums = nums;
        helper(new List<int>(), new List<int>());
        return result;
    }

    public void helper(List<int> idx, List<int> l)
    {
        if (l.Count == nums.Length)
            result.Add(new List<int>(l));
        else
            for (int i = 0; i < nums.Length; i++)
                if (!idx.Contains(i))
                {
                    l.Add(nums[i]);
                    idx.Add(i);
                    helper(idx, l);
                    l.Remove(l[l.Count - 1]);
                    idx.Remove(idx[idx.Count - 1]);
                }
    }
}

/*use array visited*/
/*
public class Solution
{
    public IList<IList<int>> result = new List<IList<int>>();
    public IList<IList<int>> Permute(int[] nums)
    {
        Helper(nums, new bool[nums.Length], new List<int>());

        return result;
    }

    public void Helper(int[] nums, bool[] visited, List<int> l)
    {
        if (l.Count == nums.Length)
            result.Add(new List<int>(l));
        else
        {
            for (int i = 0; i < nums.Length; i++)
            {
                if (visited[i])
                    continue;
                l.Add(nums[i]);
                visited[i] = true;
                Helper(nums, visited, l);
                l.RemoveAt(l.Count - 1);
                visited[i] = false;
            }
        }
    }
}
*/

 

三、思路筆記

目的為給一個陣列出陣列元素中所有的排列。

由於我想多看些不同的解法，所以我在這一題花了較多時間，

我所查到的資料有多種解法，如 DFS、BFS 以上的回溯法 (Backtracking)，

有想過搭配 Stack、Queue 來處理，但我覺得都挺複雜的。

一開始我想說可以不用到遞迴，只單用 for 迴圈即可，

但卻遇到了如果有 n 元素時，則需要 n-1 個 for 迴圈，

這種無法確定需要幾個 for 迴圈處理的，只能先考慮遞迴來處理了。

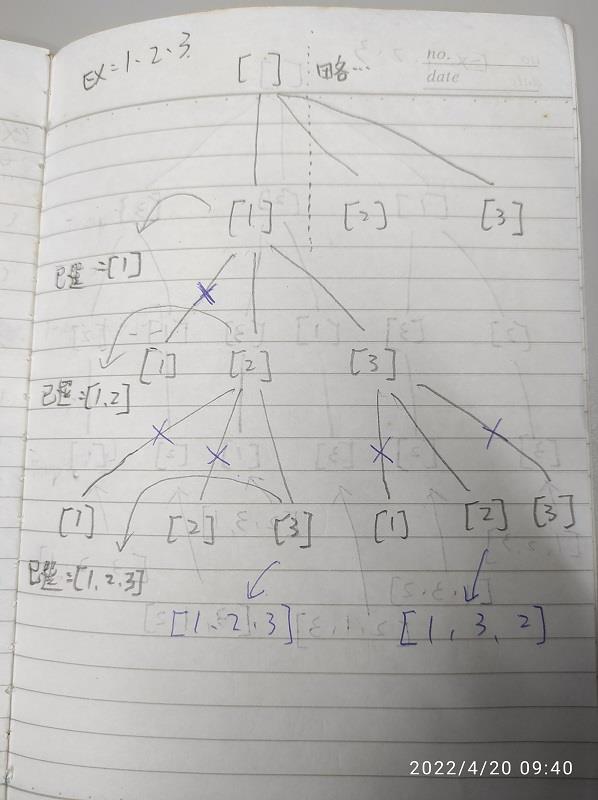
所以我個人使用我所能理解的遞迴「排除法」來做，其實就是一種 DFS 處理方式，

主要概念為將一元素添加至串列時，會先檢查該元素是否已被拿來排列，

是的話，就跳過不用他，改用下一個元素。