70. Climbing Stairs
一、題目
You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Example 1:
Input: n = 2 Output: 2 Explanation: There are two ways to climb to the top. 1. 1 step + 1 step 2. 2 steps
Example 2:
Input: n = 3 Output: 3 Explanation: There are three ways to climb to the top. 1. 1 step + 1 step + 1 step 2. 1 step + 2 steps 3. 2 steps + 1 step
Constraints:
1 <= n <= 45
二、程式作法
/*Dynamic Programming O(n)*/
public class Solution
{
public int ClimbStairs(int n)
{
return Helper(1, 1, n);
}
public int Helper(int curr, int next, int n)
{
if (n == 0)
return curr;
else
return Helper(next, curr + next, n - 1);
}
}
/*Depth-first Search O(n^2) Time Limit Exceeded*/
/*
public class Solution
{
public int ClimbStairs(int n)
{
return Helper(n);
}
public int Helper(int n)
{
if (n == -1)
return 0;
if (n == 0)
return 1;
return Helper(n - 1) + helper(n - 2);
}
}
*/
三、思路筆記
題目為每次可爬一個階梯或兩個階梯,試問共有 n 階樓梯時,則可有幾種方法爬完?
這題的解法並不適合人類理解,看完各項參考資料後,
我的解法是先理解問題後,再觀察答案的規則,
然後發現是費氐數列後,再以針對費氐數列的程式來解。
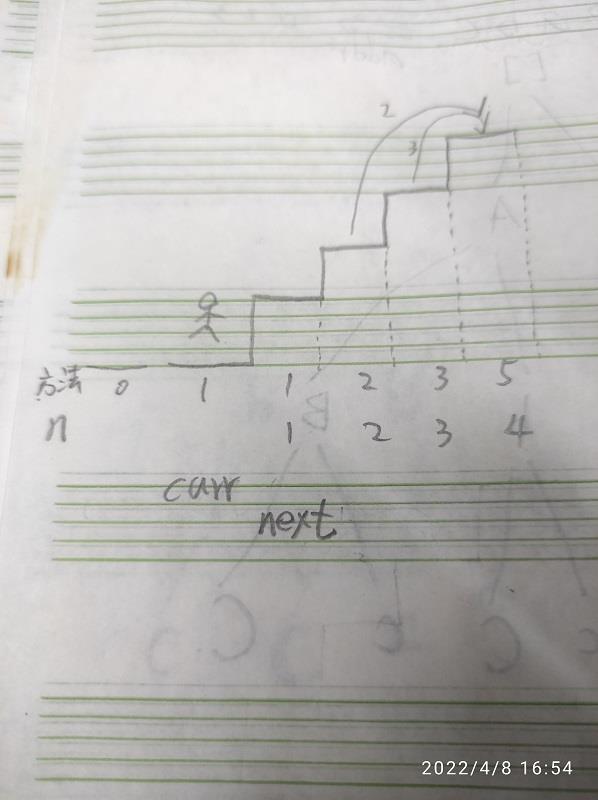
| 到達的方法 | 1 | 2 | 3 | 5 | 8 |
| 共有 n 個階梯 | 1 | 2 | 3 | 4 | 5 |