Brooke

一、題目

Given a triangle array, return the minimum path sum from top to bottom.

For each step, you may move to an adjacent number of the row below. More formally, if you are on index i on the current row, you may move to either index i or index i + 1 on the next row.

 

Example 1:

Input: triangle = [[2],[3,4],[6,5,7],[4,1,8,3]] Output: 11 Explanation: The triangle looks like:   2  3 4 6 5 7 4 1 8 3 The minimum path sum from top to bottom is 2 + 3 + 5 + 1 = 11 (underlined above).

Example 2:

Input: triangle = [[-10]] Output: -10

 

Constraints:

• 1 <= triangle.length <= 200
• triangle[0].length == 1
• triangle[i].length == triangle[i - 1].length + 1
• -104 <= triangle[i][j] <= 104

 

Follow up: Could you do this using only O(n) extra space, where n is the total number of rows in the triangle?

 

二、程式作法

 /*
 * Dynamic Programming
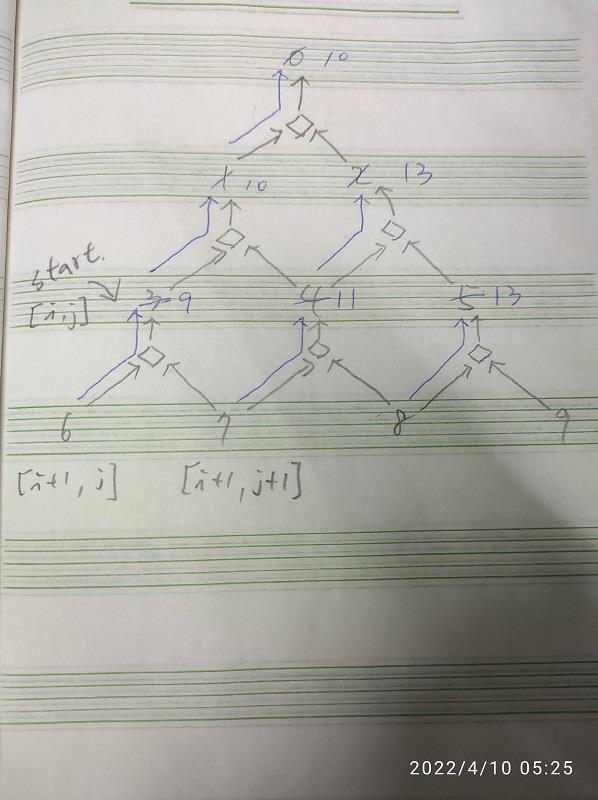
 * 由下而上往回推出答案
 */
public class Solution
{
    public int MinimumTotal(IList<IList<int>> triangle)
    {
        int i = triangle.Count - 1 - 1;
        while (i >= 0)
        {
            for (int j = 0; j < triangle[i].Count; j++)
                triangle[i][j] = triangle[i][j] + Math.Min(triangle[i + 1][j], triangle[i + 1][j + 1]);

            i--;
        }
        return triangle[0][0];
    }
}

 

三、思路筆記

我們一開始會直覺地由上往下走出最小和之路徑出來，

但會發現到一種狀況，就是每一元素底下都有兩種路徑，

如有 n 層結構則有 2^(n-1) 種的路徑結果，我們必需把整棵樹跑完，

並儲存各種路徑結果才能比較出最後答案，當層數一多時，

此種做法恐導致 Time Limit Exceeded。

可使用 Dynamic Programming 做法，

由下往上推來求解，我們會發現這是收斂狀態。