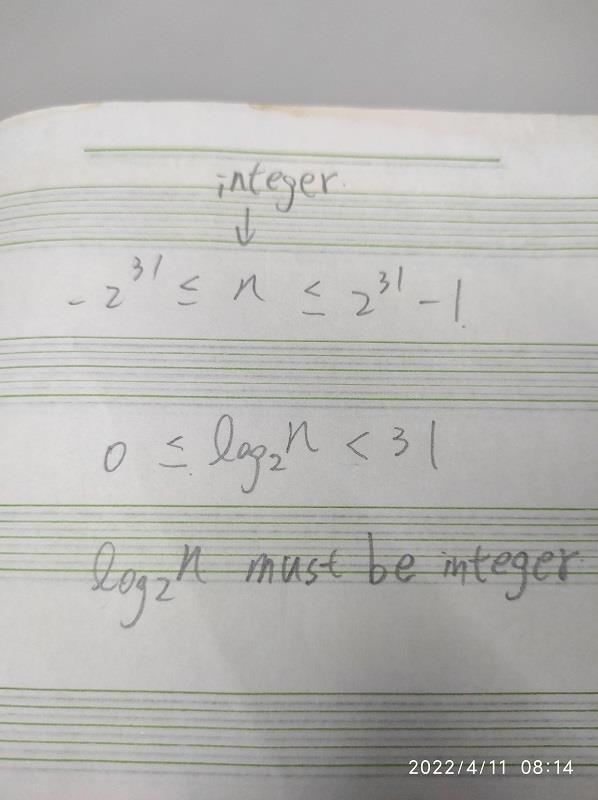Brooke

一、題目

Given an integer n, return true if it is a power of two. Otherwise, return false.

An integer n is a power of two, if there exists an integer x such that n == 2x.

 

Example 1:

Input: n = 1 Output: true Explanation: 2⁰ = 1

Example 2:

Input: n = 16 Output: true Explanation: 2⁴ = 16

Example 3:

Input: n = 3 Output: false

 

Constraints:

• -231 <= n <= 231 - 1

 

Follow up: Could you solve it without loops/recursion?

 

二、程式作法

 /*
 解法三 - 取 Log2
 */
public class Solution
{
    public bool IsPowerOfTwo(int n)
    {
        return Math.Log2(n) % 1 == 0 ? true : false;
    }
}

/*
 解法一 while loop 取 MOD
 */
/*
public class Solution
{
    public bool IsPowerOfTwo(int n)
    {
        if (n < 1)
            return false;
        if (n == 1)
            return true;

        while (n % 2 != 1 && n != 0)
            n /= 2;

        if (n == 0)
            return true;

        return false;
    }
}
*/

/*
 解法二 - for each check char array to get only 1 value
 */
/*
public class Solution
{
    public bool IsPowerOfTwo(int n)
    {
        if (n < 1)
            return false;

        string binary = Convert.ToString(n, 2);
        char[] c = binary.ToCharArray();

        int counter = 0;
        for (int i = 0; i < c.Length; i++)
        {
            if (c[i] == '1')
                counter++;
        }

        if (counter == 1)
            return true;
        else
            return false;
    }
}
*/

 

三、思路筆記

題目為找尋整數 n 是否為 2 的整數 x 次方。

目前我想到的方式有三種，

解法一，取 MOD，如果 n 是 2 的 x 次方的話，則其一定可被2整除之特性。

解法二，用二進制來表示，如果 n 是 2 的 x 次方的話，只會出現一個 1。

解法三，取 log2(n)，如果 n 是 2 的 x 次方的話，log2(n)出來必定是整數。