堅森-學習大小事

• Tree
   1. 由一個 root node 與多個 child node 組成
   2. 每個 node 的節點數量稱作 degree, 可以有多個子節點
   3. 每個 node 會記錄它的子節點是誰與在節點上儲存的資料
   4. 每個 node 只能有一個父節點
   5. 每一條分支都可以看做一條 linked list
   6. 沒有子節點的node, 又稱作 leaf node
   7. tree 當中沒有 cycle
   
• Binary Tree
  a. 每一個 node 最多只能有兩個子節點
  b. 子節點有左右之分(left node, right node)
• Binary Search Tree
  1. 左子樹上所有節點的值均小於它的根節點的值
  2. 右子樹上所有節點的值均大於它的根節點的值
  3. 任意節點的左、右子樹也分為二元搜尋樹
  4. 不會出現有重複值的節點
• Binary Tree Traversal
  a. Pre-order: root -> left node -> right node
  b. In-order: left node -> root -> right node
  c. Post-order: left node -> right node -> root
  d. Depth-First Search (DFS, 深度優先搜尋)
  • 其中, In-Order 可以也可以用來做順向(小到大)排序跟逆向(大到小)排序

******************************************************************************************

• 建立 BST
• 此範例是已知一個  array[], 要將內容建立 BST
• data[] = {17, 50, 5, 18, 3, 45, 23, 66, 2, 31};
• Insert data to BST
  • 兩種方式實作: Iterative & Recursive

BST_Node* InsertNode(BST_Node* root, int val)
{
    BST_Node *new_node = NULL;
    BST_Node *current_node = NULL;
    BST_Node *parent_node = NULL;
    new_node = (BST_Node*)malloc(sizeof(BST_Node));
    if(new_node == NULL){
        printf("new_node malloc fail!! \r\n");
        return;
    }
    new_node->left = NULL;
    new_node->right = NULL;
    new_node->data = val;
  
    if(root == NULL)
    {
        root = new_node;
        printf("new_node: %x \r\n", new_node);
        return root;
    }
    else
    {
        current_node = root;
#if 0        
        // Method: Iterative, Find the leaf node and add new_node to tree
        while(current_node != NULL)
        {
            parent_node = current_node; 
            if(current_node->data > val)
            {
                current_node = current_node->left;    
            }
            else if(current_node->data < val)
            {
                current_node = current_node->right;  
            }
            else
            {
                printf("val:%x already in BST !! \r\n", val);
            }
        }

        // break while loop: means no sub-node, so it can add new_node into leaf node
        if(parent_node->data > val)
        {
            parent_node->left = new_node;
        }
        else if (parent_node->data < val)
        {
            parent_node->right = new_node;  
        }
#else
        // Recursive method
        if(current_node->data < val)
        {
            current_node->right = InsertNode(current_node->right, val);  
        }
        else if (current_node->data > val)
        {
            current_node->left = InsertNode(current_node->left, val);
        }
        else{
            printf("val:%d already in the BST !!! \r\n", val);
        }
#endif      
    }
    return root;
}

• BST Traversal

void InOrderTraversal(BST_Node* root)
{
    BST_Node* current_node = NULL;
    if(root == NULL)
    {
        printf("InOrderTraversal: root is NULL !!! \r\n");
        return;
    }  
    current_node = root;
    if(current_node->left != NULL)
    {
        InOrderTraversal(current_node->left);  
    }
  
    printf(" %d", current_node->data);
  
    if(current_node->right != NULL){
        InOrderTraversal(current_node->right);
    }

    return;
}

// root -> left -> right
void PreOrderTraveral(BST_Node* root)
{
    BST_Node* current_node = NULL;
    if(root == NULL){
        return;
    }
    current_node = root;
    printf(" %d", current_node->data);
    PreOrderTraveral(current_node->left);
    PreOrderTraveral(current_node->right);
}

void PostOrderTraversal(BST_Node* root)
{
    BST_Node* current_node = NULL;
    if(root == NULL){
        return;
    } 
    current_node = root;
    PostOrderTraversal(current_node->left);
    PostOrderTraversal(current_node->right);
    printf(" %d", current_node->data);
}

• Find data in BST

BST_Node* FindNodeInBST(BST_Node* root, int target_num)
{
    if(root == NULL)
    {
        printf("\r\nData no in BST !!! \r\n");  
        return NULL;
    }

    BST_Node* current_node = NULL;
    BST_Node* match_node = NULL;
    current_node = root;
    
#if 0 // recursive 
    if(current_node->data > target_num)
    {
        return FindNodeInBST(current_node->left, target_num);
    }
    else if (current_node->data < target_num)
    {
        return FindNodeInBST(current_node->right, target_num); 
    }
    else
    {
        printf("\r\nFind the Node:%x !! \r\n", current_node);
        return current_node;
    }
#else  // iterative
    while(current_node != NULL)
    {
       if(current_node->data > target_num) 
       {
          printf("LEFT \r\n");
          current_node = current_node->left;
       }else if (current_node->data < target_num)
       {
          printf("RIGHT \r\n");
          current_node = current_node->right;
       }else
       {
          printf("\r\nGot it!! node:%x data:%d \r\n", current_node, current_node->data);
          return current_node;
       }
    }
  #endif
    return NULL;
}

• Sample Result

 

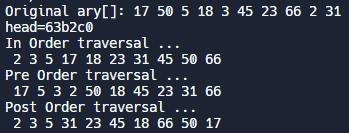
• Delete Node in BST
  • 估計是最棘手的問題了, 需要把目標刪除的點分成三種case處理:
    • 沒有 left child-node 跟 right-node
    • 有  left child-node 或是 right-node 任一點
    • 有 left child-node 也有 right-node, 這種情況下, 需要找到一個 node 來取代要被刪除的 node
      • 可以找 left child node 的最大值
      • 或是找 right child node 的最小值

// 找 right child node 的最小值
BST_Node* minimum_BST(BST_Node* root)
{
    BST_Node* current_node = NULL;
    if(root == NULL)
    {
        return NULL;
    }
    current_node = root;  
    while(current_node->left != NULL)
    {
        current_node = current_node->left;
    }
    return current_node;  
}

BST_Node* DeleteNodeInBST(BST_Node* root, int del_num)
{
    if (NULL == root){
        return NULL;
    }  

    BST_Node* current_node = NULL;
    current_node = root;
  
    if(current_node->data > del_num)
    {
        current_node->left = DeleteNodeInBST(current_node->left, del_num); 
    }else if(current_node->data < del_num)
    {
        current_node->right = DeleteNodeInBST(current_node->right, del_num); 
    }
    else
    {
        if (current_node->left == NULL && current_node->right != NULL)
        {
            BST_Node* temp = NULL;
            temp = current_node->right;
            free(current_node);
            return temp;
        }else if (current_node->right == NULL && current_node->left != NULL)
        {
            BST_Node* tmp = NULL;
            tmp = current_node->left;
            free(current_node);
            return tmp;
        }else if (current_node->right == NULL && current_node->left == NULL)
        {
            free(current_node);
            return NULL;
        }

        BST_Node* tmp = minimum_BST(current_node->right);
        current_node->data = tmp->data;
        current_node->right = DeleteNodeInBST(current_node->right, tmp->data);
      
    }
    return root;
}