上一篇提到的是對稱式加密(又稱為私密金鑰加密系統),而對稱式加密雖然速度快,但是在於確保安全的部份則顯示較為軟弱
非對稱式加密則是大大的提升了安全性的部份,而不止是在於機密性的保護,對於內容傳遞的保護則更加的嚴僅
公開金鑰的概念是在1976年由Diffie及Hellman兩人共同提出的,所使用到的有私鑰和公鑰兩種概念…
上一篇提到的是對稱式加密(又稱為私密金鑰加密系統),而對稱式加密雖然速度快,但是在於確保安全的部份則顯示較為軟弱
非對稱式加密則是大大的提升了安全性的部份,而不止是在於機密性的保護,對於內容傳遞的保護則更加的嚴僅
公開金鑰的概念是在1976年由Diffie及Hellman兩人共同提出的,所使用到的有私鑰和公鑰兩種概念
而私鑰和公鑰之間是有絕對關聯,私鑰保有了私密性(Secret)、公鑰則是提供予發散用於加解密使用(distribute)
當然有公開金鑰演算法主要是確保傳遞者的資料機密性(Confidentiality)及證明傳遞,傳遞者以接收者的公鑰將訊息加密後傳遞給接收者
接收者再以私鑰解開,傳遞的過程中因為傳遞者是以接收者的公鑰加密,因此只有接收者的私鑰能解開
加強了其保密性。下圖為確保confidentiality示意圖: 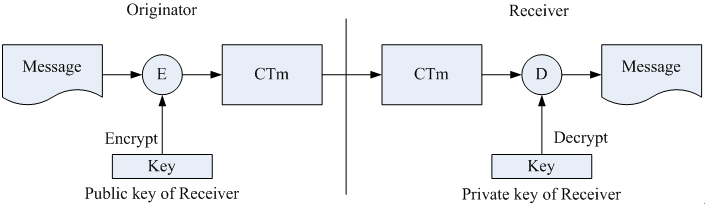
證明傳遞則是以傳送者的私鑰加密訊息,接收者以傳遞者的公鑰解密,使用者在解密的過程中,若是金鑰無法解密
則代表訊息傳遞的來源是有問題的,下者為Proof of origin示意圖: 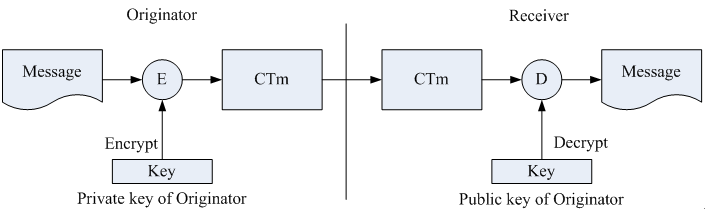
當將此二者結合,則同時可以兼具確認來源及確保機密性,下圖為其運作示意圖: 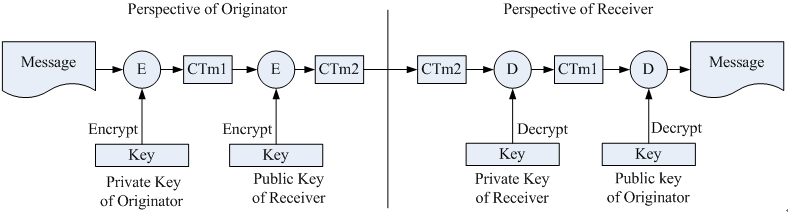
於非對稱式加密來說,由於對稱的流程並沒有像非稱式這麼複雜,非對稱式加密的嚴僅度比較夠,當然在運作上面就比起對稱來的慢
也比較不適合用於大容量的資料加密,非稱式加密還有一個特性,舉例說明像是6的k次方是1296,要推算k是很容易的,
但是3的k次方是3乘mod 13,則k的值會有4、7、10.3,這種特性就稱為hard problems,也叫做one-way trapdoor
明文加密成為密文簡單,但反推難。符合這一類的加密法有:RSA(Rivest-Shamir-Adleman), EI-Gamal, Diffie-Hellman,
ECC(Elliptic-Curve Cryptography), DSA(Digital Signature Algorithm)
RSA(Rivest-Shamir-Adleman):是公開金鑰加密系統的代表作,在金鑰的散發是源自於對稱加密,並且具有數位簽章服務的架構
開發者共有三位Ron Rivest, Adi Shamir及Leonard Adleman在1997年開發出來的加密法,預設值是1024bits,
若要安全一點,可把key sizes調整至2048bits~4096bits之間,這種加秷法是以數學上所稱的取冪模組(Modular exponentiation)為基礎的運作方式。
Diffie-Hellman:是世界上的第一套公開金鑰加密系統,於1976年設計出來,使用兩把不同的金鑰達成key exchange
使敏感的訊息得以安全的傳遞,並且保有私鑰,使加密的key不會流露在網路上。
EI-Gamal:於1984年第一次發佈出來,後續包含在PGP之中,成為一種在後端將不安全的訊息傳遞做為後續補強的利器,
並且EIGamal中包含有DSA,且加密的方式類似RSA,Key 的流通則類似Diffie-Hellman.
ECC;橢圓曲線加密法:能用於Key的流通,資料加密及數位簽章上,這種加密法非常的快速,而且key的size相當的小,
用一個比較明確的例子,1024-bit RSA = 160-bit ECC,非常的適合用於資源不足的應用程式
最有名的應用像是微軟的序號演算就是個最好的例子
而非對稱式加密,即然比較複雜以外,月什麼優缺點呢?
優點:
Confidentiality/Privacy;維持了機密性、私密性 (資料不能被非正確的私鑰解密)
Access Control;達成存取控制 (私鑰僅能用於一個個人使用)
Authentication可驗證 (可證實識別是傳輸者)
Integrity確保完整性 (資料不能被篡改)
Non-repudiation不可否認性 (傳送者無法否認曾傳遞過的資料)
缺點:
Computationally Intensive;演算過於密集
Slow太慢 (比起對稱式加密還要慢了約1000倍)
這個章節中,我們討論到了非對稱式加密的幾種常見的加密演算法,也有討論到相關的優缺點
下一篇再跟大家一起討論有關訊息完整性控制的部份,密碼學的部份除了機密性以外,最重要的就是完整性才是真正密碼學的精髓
Anything keeps Availability.
Anywhere keeps Integrity.
Anytime keeps Confidentiality.
keep A.I.C. = Information Security