何謂「直方圖」?
「直方圖」能做什麼?
如何匹配「直方圖」?
過了快一年了
終於想到blog一年沒寫了
想來想去還真不知寫什麼好
感覺會的東西都是網路上看得到的
剛好前陣子學弟問我梯度直方圖
想了下才發現那不就是HoG嗎...
所以想想還是將常用的東西用自己的方式說明
當做給數學不上不下的人另一種方式來看這些東西...
首先來寫一個什麼是直方圖及直方圖的用途吧!
何謂「直方圖」
所謂直方圖大概是長這樣
那直方圖可以做什麼呢?
例如我們要統計一個班級的身高
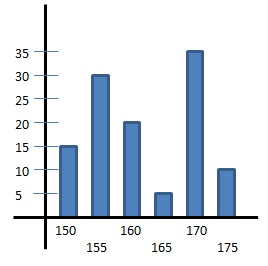
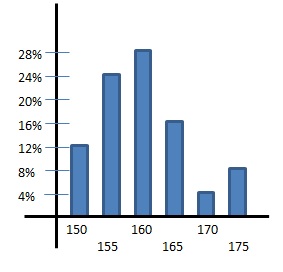
我們可以看到上面這個直方圖說明了
某個班級裡
150公分有15人 155公分有30人
160公分有20人 165公分有5人
170公分有35人 175公分有10人
簡單的來想直方圖就是統計結果的圖形呈現
當然直方圖也是一種分佈圖 (如上面的例子:身高的分佈圖)
在某些應用上我們可能需要匹配兩個不同的直方圖
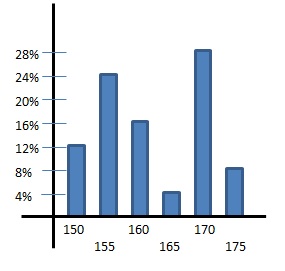
在這種情況下,通常會將直方圖做正規化 (直方圖所有值的加總等於1)
另外如果直方圖所有值的加總等於1也可以想像成是一個機率密度函數
「直方圖」能做什麼
就我所知直方圖至少能用在三種地方
1.分析
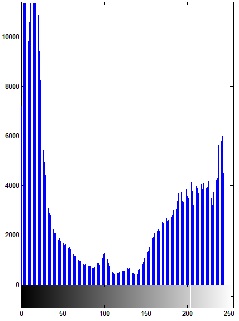
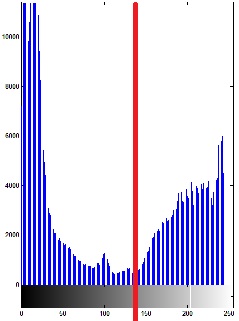
對於左圖影像我們可得到右圖的直方圖
對於這樣的直方圖我們可以得到影像的灰階分佈
藉由灰階分佈可以分析出影像的「明暗度」、「對比度」…
當然要分析的話就需要使用其它的工具來了解這張直方圖所帶來的意義
這邊只簡單說明一下藉由直方圖可以分析什麼
2.影像多值化
影像中最常用的方法之一就是影像的二值化
其中一種方法就是利用直方圖所帶來的資訊來對影像進行二值化
簡單的想法就是在峰谷的地方當成閥值對進行影像的分割
灰階值大於140的為白,小於140的為黑
當然利用類似的方式也可以將影像進行多值化
而通常進行多值化的準則「Otsu」是個不錯的方式
(題外話:影像的多值化也像一種影像的切割)
3.特徵表示
用在特徵表示上
直方圖就成了統計某種東西(顏色、身高…之類)的分佈
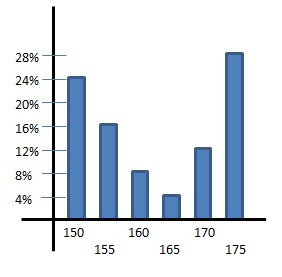
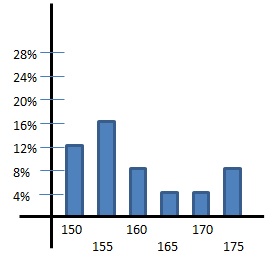
例如下面兩個不同班級的身高直方圖
如果我們現在只有身高分佈的直方圖而不知道是左邊還是右邊的班級
我們可以藉由直方圖匹配的方式
來得知這個未知班級的直方圖倒底是左邊還是右邊的班級
依這樣的思維
直方圖就成了一種特徵表示的方法了
藉由統計某種東西的分佈來表示其特徵
如著名的HoG就是統計梯度的分佈來表示特徵
如何匹配「直方圖」
在直方圖的匹配上通常我們會先進行直方圖的正規化之後才進行匹配 (並不一定要進行正規化才能進行匹配,適應用而定)
其中進行匹配最簡單的方式就是將兩個直方圖做交集運算
交集結果
如果兩個直方圖經過正規化
將交集後的直方圖的所有值進行加總而得到的就等於相似度 (如上圖的相似度約為52%)
當然這樣的匹配方式是最簡單的
其它還有如「Bhattacharyya」、「Earth Mover Distance」…等方式
(就個人的使用上比較偏好「Earth Mover Distance」這個方法
只是用在二維以上的直方圖複雜度過高
不過2012年的PAMI上Ido Leichter (paper:Mean Shift Trackers with Cross-Bins Metrics)
提出了利用卷積的方式來讓Bhattacharyya也能有類似Earth Mover Distance的效果)
新手發文如有錯誤,煩請指正!