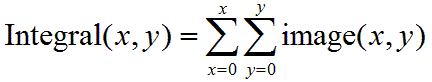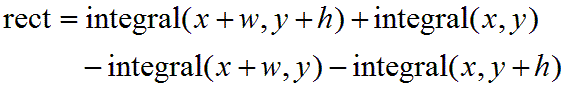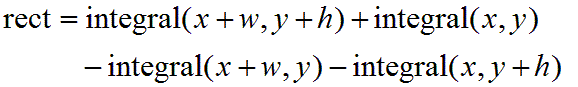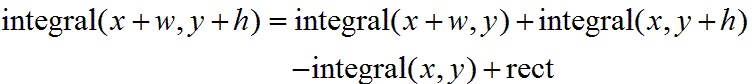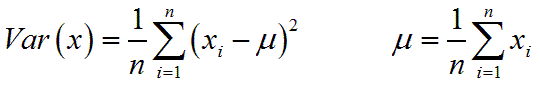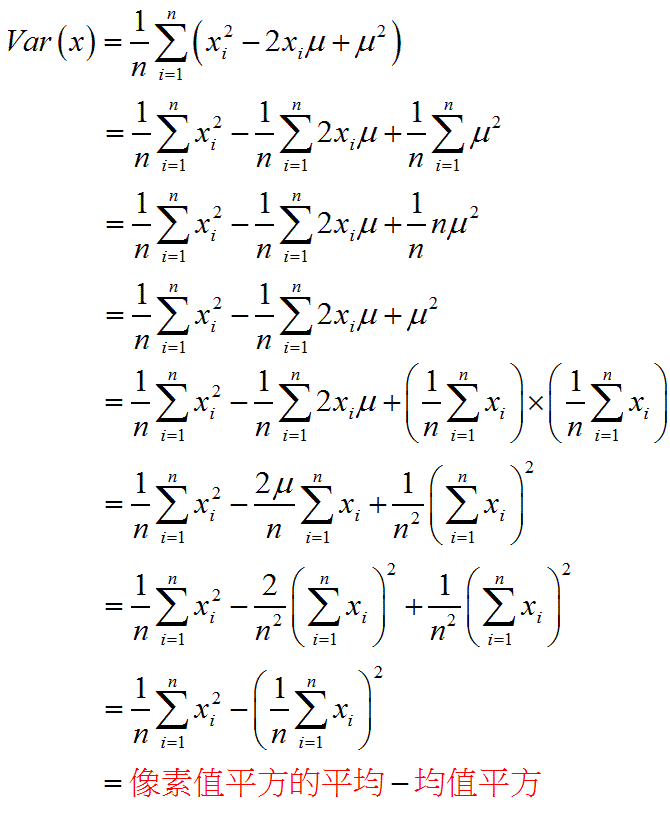Integral Image 積分影像

2013-01-18

22919
0
影像處理常用演算法
2013-11-16

「積分影像」is ?
「積分影像」的好處
如何計算「積分影像」
「積分影像」的延伸
「積分直方圖」
「旋轉45度」的積分影像
使用積分影像求「區域變異量」

「積分影像」is ?

先講古一下…(因為很難得我會去查演算法的作者是誰…)

積分影像 (integral image)又可稱summed area table (總合面積表)

是在1984年由 Frank Crow所引入到計算機圖形學中 (原始作者倒底是誰=口=)

如上面所說

「積分影像」就是將某個東西累加起來

那到底是累加什麼呢?

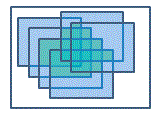
以下我們由圖來說明

以灰階影像來說

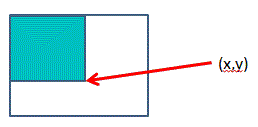
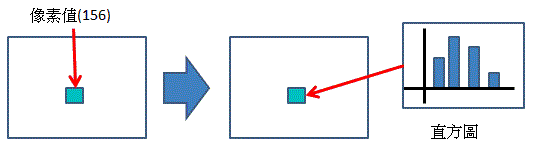
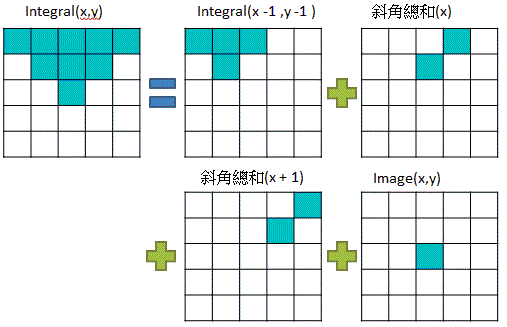
「積分影像」中點(x,y) = 從原始影像中點(0,0) 到(x,y)這個矩形內所有像素和

以數學式來表達的話

「積分影像」的好處

那倒底積分影像可以做些什麼呢

假設我們要取得影像中 x座標為 x 到 x+w 並且 y 座標為 y 到 y+h 這個矩形中所有的像素值的總和

正常就是用兩個for迴圈來計算

例：


sum = 0;
for (int i = x; i < x+w; i++)
{
    for (int j = y; j < y+h; j++)
    {
        sum += image (i, j);
    }
}

這是最直接也最簡單方式

但這樣做的話

複雜度為O(w * h)

但如果使用「積分影像」的話

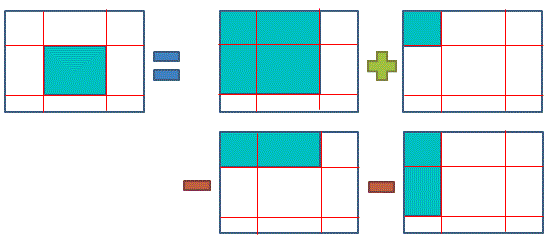
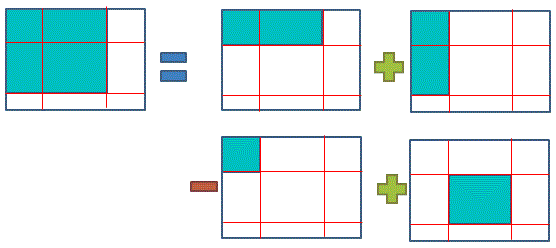
要取得這個矩形的像素值的總和只要用下面的公式

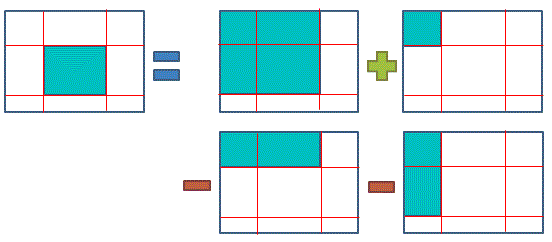
用圖來看的話

使用「積分影像」求得矩形內像素值總和的計算複雜度為O(1) (實際是O(4) 一個「+」兩個「-」一個「=」)

或許你會覺得「如果只要計算一個矩形的像素值總和」用積分影像真的會比較快嗎?

這樣不是還需要先計算出「積分影像」

因此使用「積分影像」來加速計算矩形內的像素值總和是有條件的

要計算的矩形不止一個 (通常是非常多個)
各個矩形重疊的部份非常的多

如我們要計算下面中所有矩形內的像素值總和

可以簡單的看出使用「積分影像」會有更好的計算效率

如何計算「積分影像」

`已經知道了「積分影像」好用的地方

那該如何計算「積分影像」呢

(畢竟如果計算「積分影像」每個點(x,y)都是從點(0,0)累加到(x,y)是一點效率都沒有)

從上面，我們已經知道

並且我們將rect(x,y)設為1個pixel的大小 (w =1 , h = 1)

將公式移項後得到

設定integral的範圍為-1 ~ width, -1 ~ height

integral[-1, -1 ~ height] 和 integral[-1 ~ width, -1] 都為0

我們利用部分已經計算出來的積分影像求得接下來的位置 (求解順序為由上至下、由左至右)

計算「積分影像」的虛擬碼如下


for (int j = 0; j < height; j++)
{
    for (int i = 0; i < width; i++)
    {
        integral[i, j] = integral[i - 1, j] + integral [i, j - 1] 
                         - integral[i - 1, j - 1] + image[i, j]
    }
}

因此我們可以知道計算「積分影像」的複雜度為O(width * height) (實際為O(width * height * 4))

一些小小的結論

如果我們要計算n個矩形且n個矩形所有像素點數量的加起來 > width * height * 4 + n * 4

使用「積分影像」來計算是有幫助的

後記修改：積分影像的計算應該沒有上面那麼複雜用如下的方式即可：


int sum
for (int j = 0; j < height; j++)
{
    sum = 0
    for (int i = 0; i < width; i++)
    {
        sum += image[i, j]
        integral[i, j] = integral[i, j - 1] + sum;
    }
}

複雜度會下降很多(圖有時間再補上了...)

「積分影像」的延伸

居然知道「積分影像」的好處

那積分影像是否可以應用到其它地方

而不是只有求解矩形內的「像素值總和」呢?

以下說明幾種我看過的「積分影像」的延伸

求矩形內像素值平方和 (因為這個就只是將像素值改為像素值平方就不加以說明)
「積分直方圖」
「旋轉45度」的積分影像
使用積分影像求「區域變異量」

「積分直方圖」

首先介紹比較簡單的「積分直方圖」

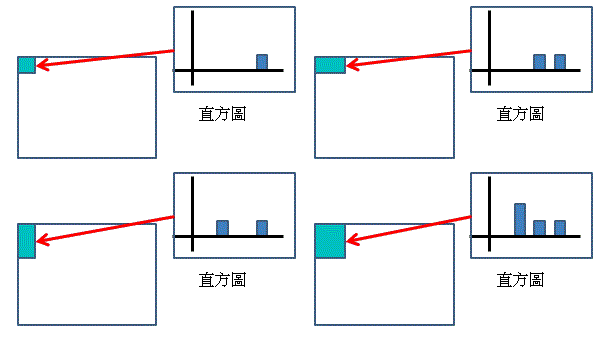
「積分直方圖」就是只是將影像的「值素值」改為「直方圖」

所以就變成累加直方圖中各個bin的總合

示意圖如下

當然這樣計算一個矩形內的直方圖的複雜度變為O(number) 實際為(number * 4) number 為直方圖的bin數

如果直方圖的bin數過高使用「積分直方圖」並不會比較好

當 bin數 * 4 > w * h

使用「積分直方圖」反會效果比較差

「旋轉45度」的積分影像

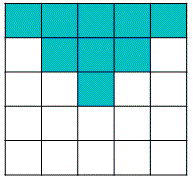
同樣的「積分影像」也能計算45度角的矩形總和

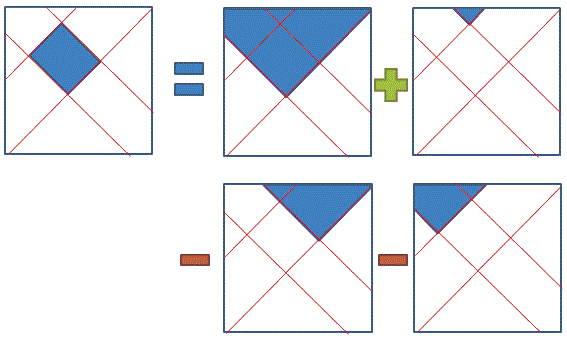
在opencv中integral45[x, y] = 右上三角形 + 左上三角形的像素總合

但在原始paper中，則為左上三角形 + 左下三角形的像素總合

其實只是方向上的差別

實際計算方式只是換個角度而已

在原始paper中計算45度的「積分影像」方法如下


for (int y = 0; y < height; y++)
{
    for (int x = 0; x < width; x++)
    {
        integral[x, y] = integral[x - 1, y - 1] + integral[x - 1, y] + image[x, y] - integral[x - 2, y - 1]
    }
}

for (int y = height - 1; y >= 0; y--)
{
    for (int x = width - 1; x >0; x--)
    {
        integral[x, y] = integral[x, y] + integral[x - 1, y + 1] - integral[x - 2, y]
    }
}

這方法需要將整張影像所有像素點計算兩次

(這方法看起來是第一次先計算左上三角形，第二次計算左下三角形

執行的順序為第一次是由上至下由左至右，第二次是由下至上由右至左

而會這樣計算是因為需要第一次計算的結果來計算第二次的值

如果先將前面(左上部份)的結果複蓋，後面(右下部份)將不能計算)

而在opencv中計算方式如下