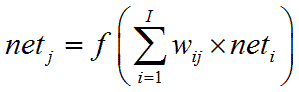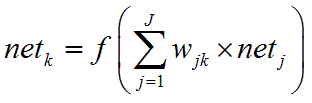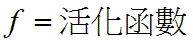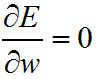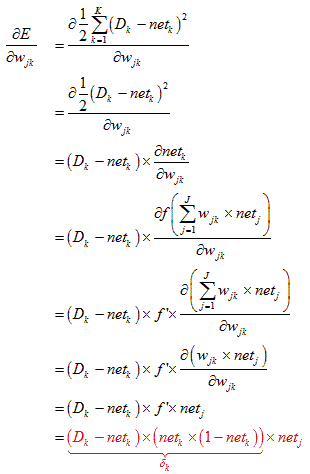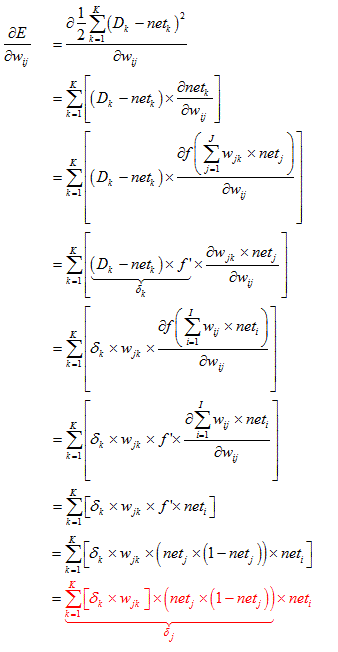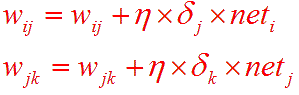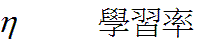學習堅持，堅持學習

About「倒傳遞類神經網路」

類神經網路是模仿生物神經網路所發展出來的演算法

而「倒傳遞類神經網路」是類神經網路的其中一種 (以下稱倒傳遞簡稱BP)

是眾多類神經網路中較具代表性的一種，屬於「監督式學習」

居然是「監督式」就代表著我們需要給「BP」一組訓練資料

利用這組訓練資料讓BP去學習「輸入特徵」及「結果」之間的關係

所以這些資料需要有「輸入特徵」及「正確結果」

 

而「BP」的功用如圖

將輸入的資料 (特徵) 丟入「BP」得到答案

一個簡單的例子

 

當然最終我們希望將「不知結果的東西」輸入到「BP」，然後由「BP」告知我們「結果」

為了讓「BP」擁有這樣的能力，因此我們需要先讓「BP」學習 (所以需要給予「輸入特徵」及「正確結果」)

就像教小孩子一樣，告訴他什麼是對的什麼是錯的

讓他經過學習後可以判斷未知的事情

 

「倒傳遞類神經網路」的架構

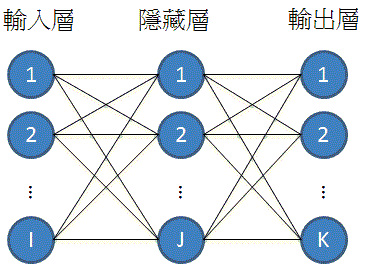
「BP」的架構如下：

整個神經網路就是一堆「線」和「圈圈」並且一層一層的連接

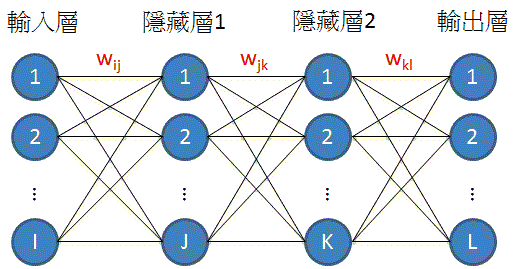
而「BP」並不限定隱藏層的數量

也可以有多層隱藏層如：

 

「倒傳遞類神經網路」神經元、連接權重、活化函數代表、用處?

神經元

隱藏層的神經元net_j                                                                                   

 輸出層的神經元net_k

簡單來說「某一個神經元 = 將前一層所有神經元乘上連接權重的總和再經由活化函數所得到的結果」

而「輸入層的神經元 = 輸入特徵」

 

活化函數

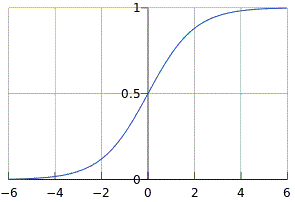
通常我們選擇活化函數為sigmoid function，函數圖形如下

活化函數扮演著非常重要的角色

活化函數需為非線性的函數 (如果活化函數為線性函數，多層網路和單層網路並沒有差異)

活化函數需為可微函數 (在調整權重時需要對活化函數微分)

事實上也是因為活化函數的存在，神經網路才能解決非線性問題

 

連接權重

而連接權重w_ij = 神經元 i 的資訊對於神經元 j 的重要程度

可以想成權重越高重要性越高

 

以一個簡單的想法來說明整個架構：

假設神經元     = 人
輸入層神經元 = 基層員工
隱藏層神經元 = 中階主管
輸出層神經元 = 最高主管

我們可以想成

對中階主管來說，某個基層員工所給的資訊重要性不同 (即為連接權重)
並且中階主管會統整所有基層員工的資訊，再經由自身決定資訊的重要性(活化函數)

同樣的對最高主管也是做相同的事情

 

「神經元」和實際問題的對應

那對於一個實際的問題「輸入層神經元」和「輸出層神經元」又對應到什麼呢?

輸入層神經元

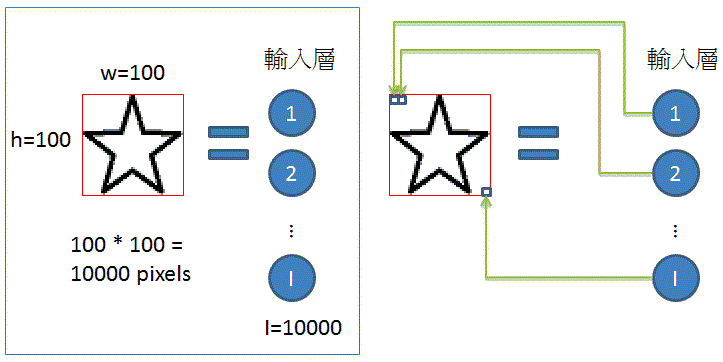
如果我們輸入一張100*100的圖

每一個pixel就對應到一個「輸入層神經元」

所以輸入層神經元的個數 = 圖片的pixel數

確實的來說

每個輸入層的神經元代表著輸入資料的一個特徵

 

輸出層神經元

那如果我們要將輸入的圖分成三類 (假設是「star」、「pentagon」、「rentangle」)

那「輸出層神經元」分別對應到每個類的相似度

 

 

「倒傳遞類神經網路」的兩個階段

從上面稍微了解「BP」的架構及各東西代表的意思後

接下來說明一下「BP」的兩個階段，分別是「學習階段」、「回想階段」

 

學習階段

那對於「BP」的學習到底是要學習什麼呢?

對於「學習階段」來說

輸入層神經元    已知    (訓練資料)
連接權重           未知
輸出層神經元    已知    (訓練資料)

因為我們有「輸入資料」也有「目標輸出結果」

學習階段就是要找到一組連接權重

讓輸入資料經過這組連接權重得到目標輸出結果

 

回想階段

而經過學習的「BP」就能讓我們拿來處理問題

所以輸入一個資料，我們有了

輸入層神經元    已知    (輸入資料)
連接權重           已知    (經由訓練得到)
輸出層神經元    未知    

所以在「回想階段」就是利用

「輸入資料」和訓練出來的「連接權重」，計算出「結果」

 

如何訓練「倒傳遞類神經網路」

「BP」是依照最小誤差平方來進行權重的訓練

訓練的流程如下：

1. 初始化權重 (random)
2. 利用目前的權重計算輸出結果
3. 計算輸出結果和目標結果的誤差
4. 調整權重
5. 重複2~5直到收斂

計算輸出結果

利用

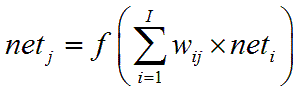     和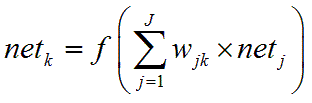     

從「輸入層神經元」一層一層的計算到「輸出層的神經元」

 

計算輸出結果和目標結果的誤差

誤差的1/2只是為了微分的方便加上的

 

調整權重

因為有了誤差E，要調整權重w_ij 和w_jk

我們可以使用微分的方式讓

(懶的看推導，請直接看紅色公式)

對於隱藏層到輸出層的權重w_jk調整

 

對於輸入層到隱藏層的權重w_ij調整

重點就是用兩條紅色的公式來求得w_ij和w_jk造成的誤差

 

實作後發現的小發現

以下實作後課本上發現的一些小細節，可能是課本沒提或是我沒看到…

• sigmoid function的範圍
  
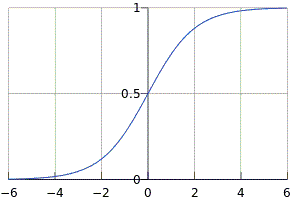
  從這圖可以發現輸入值的範圍在正負6以後就不太會改變了
  但以隱藏層的神經元為例
  
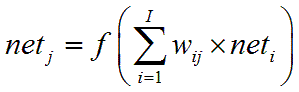
  我們會將前一層的所有神經元乘上權重在如總起來
  非常容易就超過正負6的範圍
  因此將
  
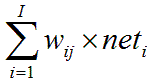
  限定在範圍 (正負6) 內是很重要的
  如果不在這個範圍內會有不容易收斂的情況
   
• 基於上面的問題
  將輸入層神經元正規化後
  可以減少這種情況的產生
  如灰階影像中某個pixel值為0~255 改為0~1

 

結論

整理一下重點

1. 「BP」為「監督式學習」需要一組有「輸入特徵」及「目標結果」的訓練資料
    
2. 輸入層神經元 = 輸入特徵
   輸出層神經元 = 分類結果 (對某類的相似度)
    
3. 「BP」主要分為兩個階段「學習階段」、「回想階段」
   學習階段 - 找到合適的權重讓輸入特徵可以計算出目標結果
   回想階段 - 利用學習完的特徵計算結果
    

另外還有一些進階技巧

1. 隱藏層數目
2. 隱藏層的神經元數
3. 學習速率
4. 活化函數選擇

等就需要去網路上自己慢慢觀看了…

 

新手發文如有錯誤，煩請指正！