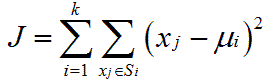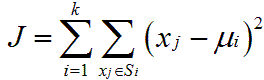學習堅持，堅持學習

「K means」的用處

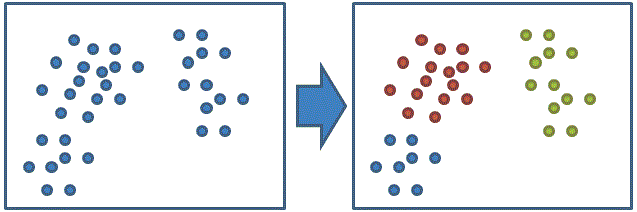
「K means」是一種聚類 (Cluster) 的方式

聚類基本上就是依照著「物以類聚」的方式在進行

(或許我們也可能想成，相似的東西有著相似的特徵)

給予一組資料，將之分為k類 (k由使用者設定) 就是「K means」的用處

從數學式來看，「K means」主要是為了將下列公式最小化

所有資料點 x_j 到其對應群中心 u_i 的距離總合是最小的

目的就是要找到最佳的群中心 u_i 及 x_j 所屬的群來符合上面的要求

 

「K means」流程

為了解決

這個公式

「K means」使用兩步驟的疊代方式求解 (直接微分難度有點高阿…)

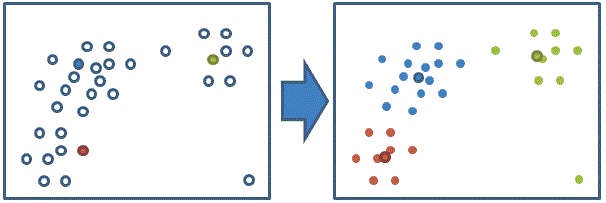
完整的流程如下

1. 隨機選取資料組中的k筆資料當作初始群中心u₁~u_k 
   
    
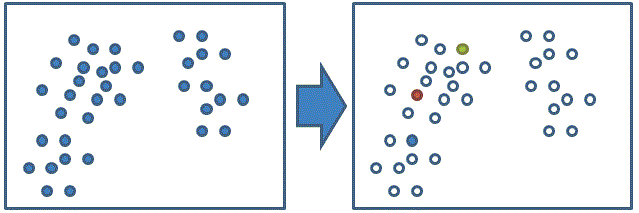
2. 計算每個資料xi 對應到最短距離的群中心 (固定 u_i 求解所屬群 S_i)
   
                                                                                                                         (有框的為群中心)
   
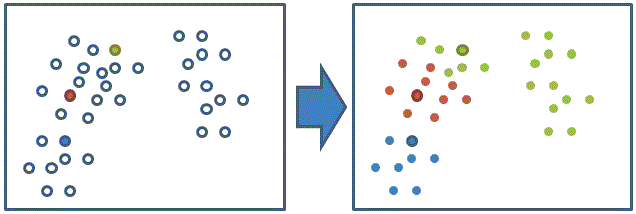
3. 利用目前得到的分類重新計算群中心 (固定 S_i 求解群中心 u_i)
   
    
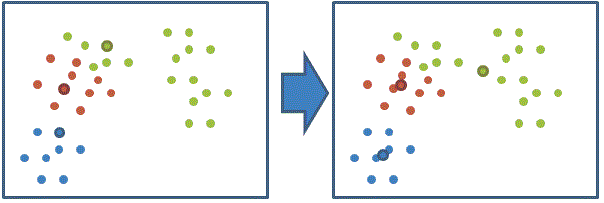
4. 重複step 2,3直到收斂 (達到最大疊代次數 or 群心中移動距離很小)

 

初始值設定

大概了解了「K means」的流程之後

我們可以發現一開始的群中心是不固定的

也就是說同一筆資料用「K means」跑10次，10次的結果可能都不同

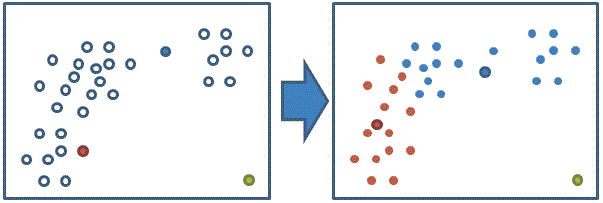
讓我們來看一個極端點的例子

由上圖可以發現

如果初始群中心設定的不好可能導致不會的結果

但就正常情況而已，

「K means」算是"速度快"、效果又不差的演算法

 

延伸

基本上「K means」算是一個非常簡單的算法，

這個算法除了讓我們將一組資料丟入，得到每個資料對應的群及群中心還可以做什麼呢?

換個想法，

1. 如果我們先用一組資料來訓練出群中心 (訓練階段)
2. 之後每丟入一個資料我們都可以找到其對應的群中心 (回想階段)

在這個情況「K means」已經有點像分類器在使用了

差別在我們只知道丟入的資料和哪個群相似，但不知道該資料明確的分類

當然之後每丟入一個資料我們也可以再次更新群心中 (online K means版本)

 

另一個想法，

如果我們有一組特徵資料，我們想知道用這組特徵來做分類是好還是不好

我們可以用「K means」來做簡單的確認

在這情況下

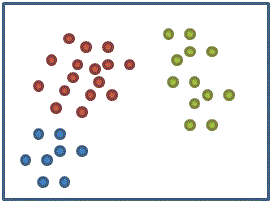
我們有特徵資料及每個資料所屬的類別

(原始特徵資料對應的分類)

接下來我們利用「K means」重新進行聚類

(利用K means的聚類結果)

就可以知道這組特徵是否容易將不同類別的資料聚在一起 (上圖聚類結果很好，沒有將分屬不同類別的資料聚在一起)

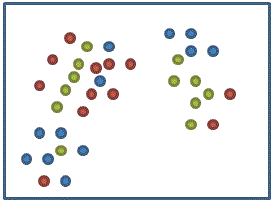
如果如下面的情況

(原始特徵資料對應的分類)

我們可以發現原始類別和「K means」的聚類結果差距很大

實際上我們可以解讀為

這組特徵或許沒有很好的表達能力 (目標類別的表達)

因為正常情況下

同類別的東西會有相似的特徵 (特徵相似 = 資料點鄰近)

而上圖中看不出這個情況

因此我們可以認為這組特徵或許不適合用來表達目標分類情況

 

新手發文如有錯誤，煩請指正！