學習堅持，堅持學習

影像處理筆記

2014-06-21

BRIEF - Binary Robust Independent Elementary Features

  • 3692
  • 0
  • 2015-09-12

特徵點
如何「描述」特徵
如何「比對」描述符
「點對」如何產生
程流
BRIEF的問題
實際應用

此篇文章主要是介紹BRIEF這個算法，
如要了解完整的內容請參閱：
BRIEF: Binary Robust Independent Elementary Features (conference)
BRIEF:Computing a Local Binary Descriptor Very Fast (journal)
此兩篇文章。
 
特徵點
在影像處理中，常會需要取得特徵來進行更多的處理，
但到底什麼是一張圖中的特徵呢?
 
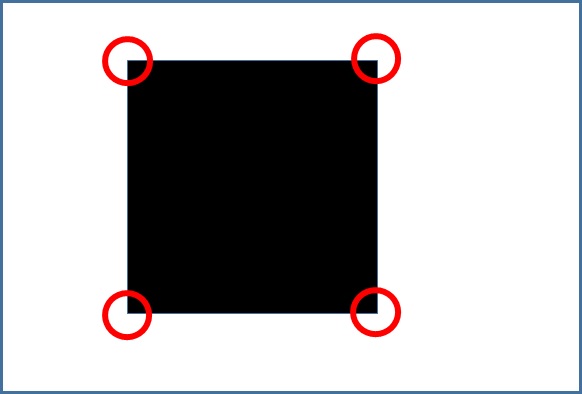
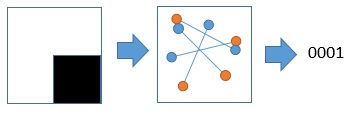
利用以下的圖來稍為做一下介紹
 
圖中的紅色圈圈即為特徵點，
這些點不就是角點嗎?
沒錯！通常的情況下影像的特徵點 = 角點，
這是因為角點更能表示其圖形的特徵，
且不受縮放的影響，
像一個五角形的圖形，
人們更會注意到他有5個角，而不是10個邊。
 
如何「描述」特徵
知道了特徵點後，
要如何分辨出不同的特徵點，
成了另一個問題，
如上圖中的4個角點，
我們知道這4個角點是不同的，
但我們要用什麼樣的方式去「描述」，
才能讓電腦分辨出這4個角點的不同?
然而特徵點又不是只有這4種，
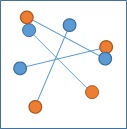
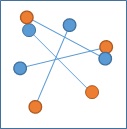
以下的圖都可能為一個特徵點，
除了我們認知的一般角點以外，
也可能會有漸層式的特徵點，
或是其它不同類型的角點，
當然有些例子可能太過誇張，
這邊想表達的是，
特徵點雖然等於角點，
但並不是只有方方正正的角才是特徵點，

所以該有效的描述特徵點，
才能讓不同的特徵點有不同的特徵值，
則是此文章主要探討的問題，
這部份有非常多的方式，
此文章只針對BRIEF做說明，
 
  1. 首先取得特徵點周圍s*s個點(BRIEF中取7*7)為其描述範圍
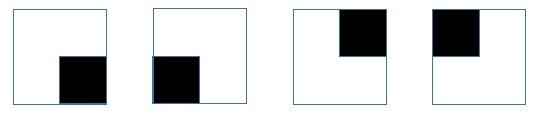
  2. 利用「點對」進行描述
    首先假定有4個「點對」如下：

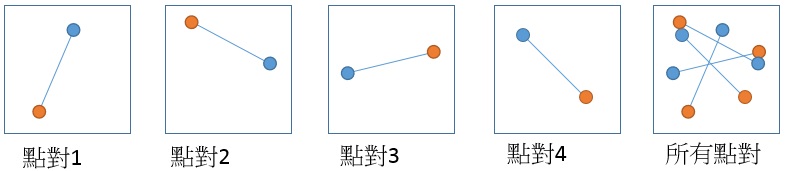
    每個「點對」存有「兩個位置」(藍色點和橘色點)，
    BRIEF則利用兩個位置其像素值之比較來進行特徵描述，
    描述的方式如下：
    當「橘色點的像素值 < 藍色點的像素值」為1，否則為0(白色點為255，黑色點為0)
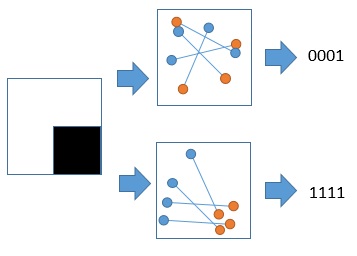
    將「點對」套用到上面的4個特徵點的結果如下：

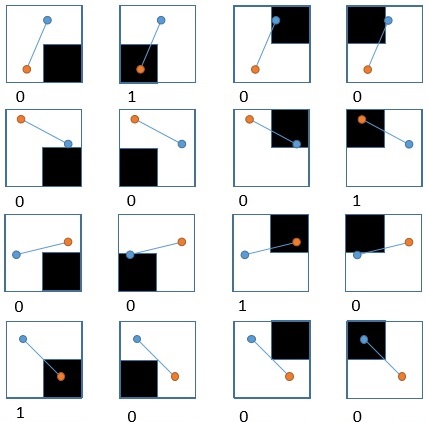
    再將所有的點對結果組成一個二元字串


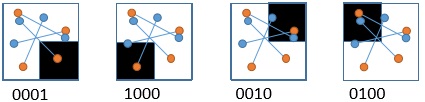
    如此，就可藉由產生的二元字串來分辨不同的特徵點
 
如何「比對」描述符
產生了二元字串之後，
我們也能藉由二組二元字串的比對來得知兩個特徵點是否相似，
而比對的方式則是先將兩組二元字串做xor運算，
再計算共有幾個bit的值為1，如：
第一組二元字串 = 1001，
第二組二元字串 = 1101，
xor的結果           = 0100，
bit為1的數量      = 1;
 
第一組二元字串 = 1101，
第二組二元字串 = 0011，
xor的結果           = 1110，
bit為1的數量      = 3;
 
如果bit為1的數量越小，
代表兩個特徵越相似，
反之越不相似。
 
「點對」如何產生
了解了整個描述的方式，
但這之中卻還有另一個問題，
「點對」是如何產生的?
在BRIEF中共提出了5種方式來產生點對，
當然這5種方式都是利用隨機產生，
只是利用不同的機率分佈進行隨機產生的方式，
以下(x，y分別代表藍色點及橘色點的位置)


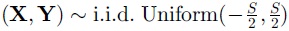
  1. x，y分別在同一個均勻分佈下進行隨機採樣


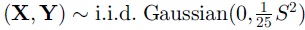
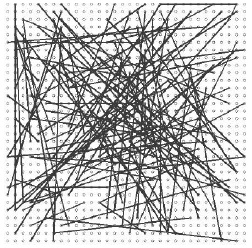
  2. x，y分別在同一個高斯分佈下進行隨機採樣


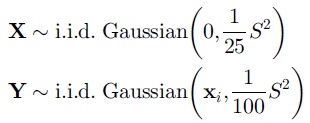
  3. x在一個高斯分佈下進行採樣，y則以x為中心點在另一個高斯分佈下進行隨機採樣

  4. 利用極座標(theta, distance)的方式來隨機採樣

  5. x固定為中心點，y則是極座標上所有可能的點

     
BRIEF中分別利用此5種規則去產生「點對」，
並且利用實驗的方式來了解哪一種方式產生的「點對」較好，
從實驗結果來看前4種各有好壞，而BRIEF是推薦使用第2種，
 
再者，雖然「點對」是隨機產生的，
但在產生第一次以後點對則是固定，
例如，我們先隨機產生「點對集」如下，

對於每個角點的描述都要使用同樣的「點對集」，
如果我們利不同的「點對集」則無法有效的分辨各個特徵點，
因為他們取得到的二元字串是不同的，如：
 
程流
最後讓我們統整一下整個BRIEF的流程
  1. 利用隨機分佈產生「點對集」
  2. 取得角點周圍s*s個點
  3. 利用「點對集」取得二元字串
  4. 匹配二元字串，利用兩個二元字串做xor運算後，bit為1的數量

 

BRIEF的問題

BRIEF存在幾個問題，這邊只稍為介紹，

  1. 利用單個pixel進行比較，抗noise能力不好
    論文中也提到可以先對影像進行smooth再取得pixel value
     
  2. 不具縮放及旋轉不變性
    對於同樣的特徵點，如果進行30度的旋轉，
    得到的二元字串將會不同，
    當然如果特徵點被縮放過也會得到不同的二元字串。

實際應用

這部份也不知該從何講起…
還是直接用圖來說明吧…
假設我有一個樣板

以及一個要檢測的影像

利用匹配我們能找到兩張影像中，
哪些特徵點是相似的

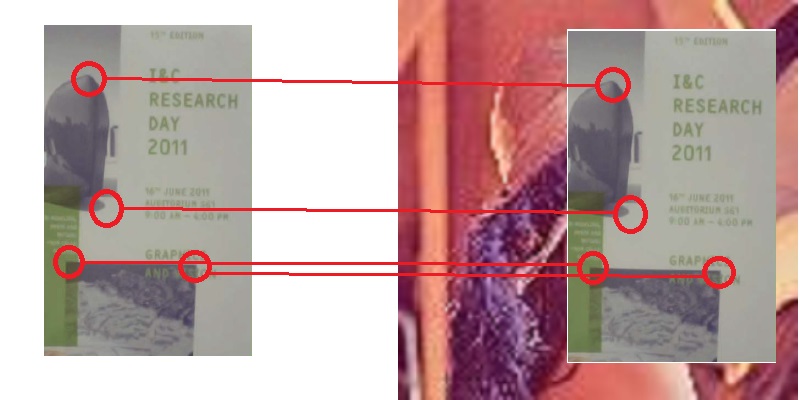
如此，便能找到樣板在該影像的位置，
當然還有其它更多的應用，這邊只是舉例一個來說明。

 

新手發文如有錯誤，煩請指正！