Neural Network 的概念探討
前言
上一次我們以十幾行程式完成阿拉伯數字的辨認,心情應該會小小波動一下(應該還不到小鹿亂撞的地步),如果我們以傳統的程式解法,不寫個幾百行,應該是不會罷手的,但是,第一次接觸 Neural Network 的朋友應該對程式碼內的函數及其參數有很多的問號,例如(先請在這裡下載並開啟 0.py 程式,對照說明):
- 第16、18行的 Dense、activation 是甚麼東東? 為何是 relu、softmax,各代表何意義?
- 第21行的 損失函數(loss) 為何使用 categorical_crossentropy,優化方法(optimizer)使用 adam 及成效衡量方式(metrics) 為何使用 accuracy?
- 第24行 Y 為什麼要預處理為 one-hot encoding 格式?
最重要的是,為什麼 『十幾行程式透過甚麼原理』能準確辨識阿拉伯數字? 以下,我們就要從頭開始講起,其中涉及機率統計、矩陣運算、線性規劃、微積分等,筆者會盡量以圖表說明,不會有任何數學公式推導,讀者不需有太大的心理負擔(我不會把你當掉, 哈哈),如需再深入,歡迎留言,筆者會盡力彌補不足之處,若尚有未逮,只能怪筆者能力不足了。
特別說明,筆者不是學者,本文所有名詞定義以淺顯易懂為最主要考量,如有不精準或謬誤之處,還請包容,也請不吝指正。
Machine Learning 概念
Machine Learning 演算法(Algorithms) 不只有 Neural Network,還包括 K-Means、Support Vector Machines(SVM)、Decision Tree、... 等等,基本上,都是希望透過資料分類(Classification)或分群(Clustering) 的方式,轉換為規則或知識,一般進行的步驟如下:
- 訓練:首先將已知的歷史資料,依資料特徵(譬如性別、年齡),將樣本作分類(譬如男人、女人、小孩),這就是所謂的訓練(Training)。
- 建立模型(Model):訓練之後,我們就會得到一個模型(簡略的講,就是公式),推算未知的資料是哪一類,例如性別是男,年齡大於18歲,模型就推斷他是男人;反之,年齡小於18歲,不論性別,模型就推斷他是小孩。
- 評估(Evaluation):隨機抓一部分的已知資料,測試模型的準確率(或其他評估指標,如 precision and recall),確定模型是堪用的,這就是『驗證』(Validation),有了評估指標,我們就可以跟老闆或客戶,拍胸脯、打包票,不準就切腹自盡(千萬不要喔)。
- 預測(Prediction):有了以上模型後,一個未知的人進來後,我們就可以依據性別及年齡推斷,他/她是男人、女人或小孩? 但是,注意! Machine Learning 不是以程式撰寫明確的規則(If ... Then ...Else),而是『以已知的資料推斷未知的資料』,只要,不斷餵資料,機器就慢慢的變聰明了。
Neural Network 概念
Neural Network 是參考生物神經系統的結構,神經元(Neuron)之間互相連結,由外部神經元接收信號,再層層傳導至其他神經元,最後作出反應的過程。
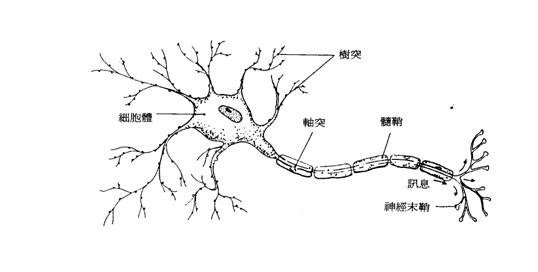
圖. 神經元構造,圖片來源: 類神經網路初探 基本架構與感知器
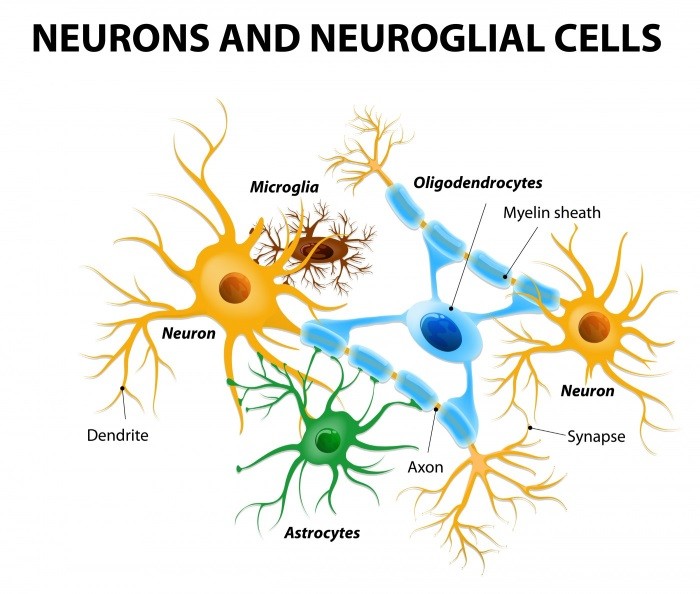
圖. 神經組織,圖片來源: Study of Dendrimers in Cerebral Palsy Animal Model Points to New Therapeutic Target
將神經系統抽象化後,就類似以下結構,這就是 Neural Network 的概念。如下圖 Input Layer 就是接收信號的神經元,Hidden Layer 就是隱藏層,而 Output Layer 就是做出反應的輸出層,而各神經元傳導的力量大小,稱為權重(Weight, 以W表示),也就是模型要求解的參數,如果求算出來,我們就得到一道公式,只要輸入信號,經過層層傳導,就可以推斷出結果了。
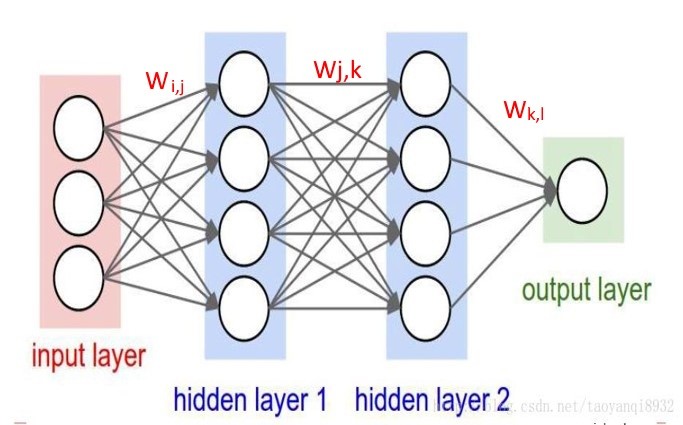
圖. 人工神經網路,圖片來源: 計算機視覺與卷積神經網路
Hidden Layer及Output Layer上每一個節點(圓圈)的值等於上一層所有節點的加權總和,如下圖左,這個公式是不是有點熟悉? 它就是統計學的簡單迴歸(Regression),迴歸要計算權重值(W),我們可以用『最小平方法』(Least Square),最小化『預測值與實際值的差距之平均值』(如下圖右),或者使用『線性規劃』(Linear Programming) 最小化目標函數,也可以求得W。
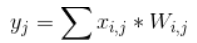 |
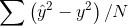 |
|---|---|
| 圖. 簡單迴歸(Regression) | 圖. 預測值與實際值的差距之平均值 |
但是,上述模型只能解決線性分類,切割過於簡單,Neural Network 作了以下的強化,以解決一般性的問題:
- 在上述的公式前乘以一個非線性函數(g),稱為 Activation Fuction,變成以下公式:
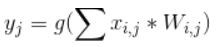
Activation Fuction有很多種,可依據問題的本質,挑選適合的函數訓練模型,請參閱下圖,Sigmoid 函數就能使Y的範圍限制在[0,1]之間,中間只有一小段模糊地帶,適合用於二分法(真或偽),另外 softmax 函數,可以將Y轉為機率值,且所有類別的機率總和等於1,就適合多分類,最大值就代表可能性最大;上次還有用到 relu函數,它是忽視負值,Y的範圍限制在[0, ∞]之間,還有其他函數,就是依照資料及模型的特性挑選就對了。
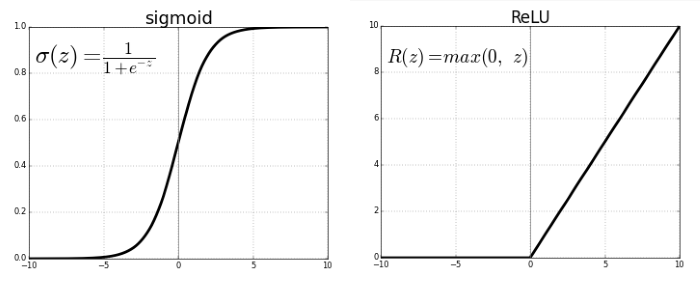
圖. Activation Functions,圖片來源:Activation Functions_Neural Networks
- 可以使用更多層 Hidden Layer,模擬生物神經系統,使學習效果更顯著,通常超過2層的 Hidden Layer,我們就稱之為『深度學習』(Deep Learning)。
模型經過以上的強化,我們就沒辦法用單純的數學公式推導,求出權重(W),因此,一般會改用『梯度下降法』(Gradient descent),以逼近法求解,這就是優化(optimization)的過程。梯度下降法就好比『我們在山頂,但不知道要下山的路,於是,我們就沿路找向下坡度最大的叉路走,直到下到平地為止』,要找到向下坡度最大,在數學上常使用『偏微分』(Partial Differential),求取斜率,一步步的逼近,直到沒有顯著改善為止,我們可能已經找到最佳解了,過程可參考下圖說明。
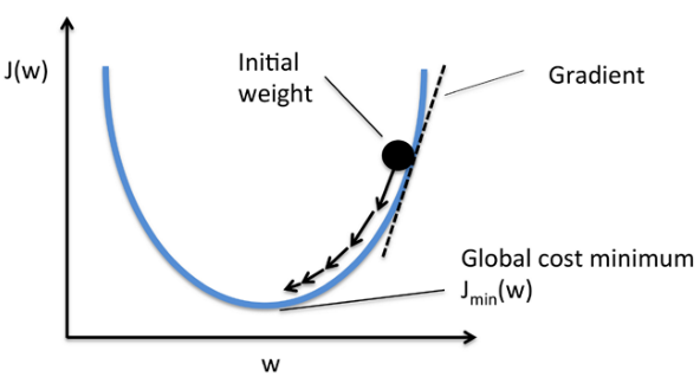
圖. 梯度下降法(Gradient descent),圖片來源:Batch gradient descent vs Stochastic gradient descent
程式解說
希望以上說明,沒有讓你搞昏頭了,Neural Network 的處理流程如下:
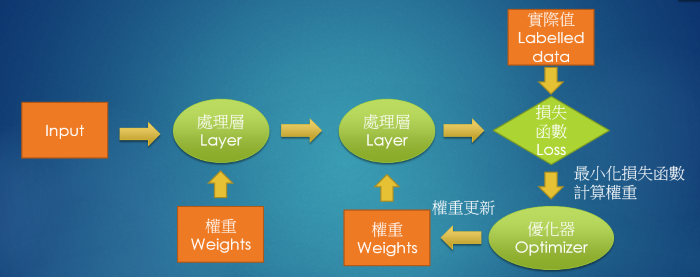
圖. Neural Network 處理流程
請對照上次的程式碼,我們要詳細解說程式結構了:
-
面對一個問題,我們要先定義要解決問題的目標,如果是損失(Loss),通常的目標就是要使它最小化,程式碼的第21行,loss='categorical_crossentropy',就是選擇損失函數(Loss Function)的種類;同時定義模型計算出來,我們要評估的成效指標,是要以『準確率』、『錯誤率』、『召回率』(Recall)或其他指標來衡量,Keras 提供的衡量指標只有各式的準確率,但可以自訂衡量指標。
-
再依每一層(Keras 稱為 Dense)的特性及需求,指定 Activation Function,例如第16行,Input Layer至Hidden Layer,我們排除負值,採用『relu』, Hidden Layer 至 Output Layer 使用『softmax』,求取每一個數字(0~9)的預測機率。kernel_initializer='normal',表示梯度下降求解的起始值,這裡選擇使用『常態分配』的亂數值,請參考 https://keras.io/initializers/ ,起始值選擇不佳,可能會影響求解的速度與答案,通常不要選太奇怪的值就好。
-
第24行 將已知資料的結果(Y)作預處理,將Y值轉成10個數字,每個數字為0或1,例如7就轉為0000000100,代表它是 0~9 十個分類的哪一個,這樣才能作矩陣運算。
-
第35行 進行模型訓練,由於損失函數可能是一個非常複雜的曲線,或逼近最佳解的幅度過小,都會使得優化速度過慢或不穩定,所以我們要限制求解的最大訓練週期(Epochs),以免跑不完。另外,梯度下降若每次都使用全部資料求斜率,可能會花費太多時間,所以通常會採用隨機抽樣,分批求解,batch_size就是指定一批要抽多少樣本。
-
第44行使用 predict_classes 函數,得到最大機率值對應的阿拉伯數字,就是預測的結果。
所以,一個模型的好壞取決於我們採用何種『損失函數』、『成效衡量指標』(Metrics)、Activation Function、優化器(optimizer)、隱藏層數(Layers或Dense)、kernel_initializer以及它們使用的參數,這些都是要依據需求反覆實驗,才能得到較好的模型,使預測更準確。因此,有人說 Neural Network 預測能力驚人,但每個人預測的成效可能都不同,聽起來,資料科學家像算命師,檔次不同,就有不一樣的結果,所以,筆者個人認為一定要了解運作原理,才能駕馭這個強大的工具。建議拿到問題時,先不要忙著解題,最重要是多作實驗,與資料先培養感情,再擬定方向,解決問題。
這次讀起來應該很累人,其實我已經忍痛刪了很多的內容,希望你還不會因此而轉台,下一篇我們就輕鬆一點,針對上次程式作一點有趣的實驗。