Code Bank

前言

之後我們會討論到各種演算法及應用，使用到的函數及其參數會更多，因此，有必要先打好基礎，將 Keras 架構及習慣用法(Convention)弄清楚，以免迷失在網海中，同時，我們也為第二篇的程式做個總結。

我們再回顧一下， Neural Network 處理流程，步驟如下：

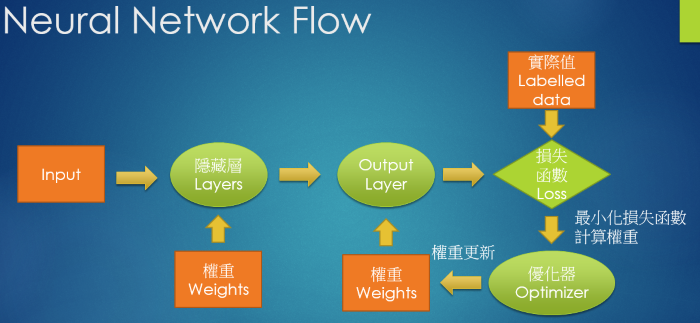
圖. Neural Network 處理流程

1. 建立模型(Model)：參見上圖，首先，我們要確立Input格式、要經過幾層處理、每一層要作甚麼處理，例如以下程式：

# 建立簡單的線性執行的模型
model = Sequential()
# Add Input layer, 隱藏層(hidden layer) 有 256個輸出變數
model.add(Dense(units=256, input_dim=784, kernel_initializer='normal', activation='relu')) 
# Add output layer
model.add(Dense(units=10, kernel_initializer='normal', activation='softmax'))

2. 確立目標及求解方法：以compile函數定義損失函數(loss)、優化函數(optimizer)及成效衡量指標(mertrics)。

# 編譯: 選擇損失函數、優化方法及成效衡量方式
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) 

2. 訓練：以compile函數進行訓練，指定訓練的樣本資料(x, y)，並撥一部分資料作驗證，還有要訓練幾個週期、訓練資料的抽樣方式。

# 進行訓練, 訓練過程會存在 train_history 變數中
train_history = model.fit(x=x_Train_norm, y=y_TrainOneHot, validation_split=0.2, epochs=10, batch_size=800, verbose=2)  

3. 評估(Evaluation)：訓練完後，計算成效。

# 顯示訓練成果(分數)
scores = model.evaluate(x_Test_norm, y_TestOneHot)  

4. 預測(Prediction)：經過反覆訓練，有了可信模型後，我們就可將系統上線使用了。

# 預測(prediction)
predictions = model.predict_classes(X)

以下我們就針對以上流程所使用到的函數，作比較詳盡的說明，但僅限於第二篇使用到的函數，如果要全方面研讀，還是要到官方網站閱讀，筆者採取的方式是『每次討論一個演算法，才說明該主題使用到的函數』。

Keras 模型類別

依據官方文件 說明，Keras 提供兩種模型:

1. Sequential Model (順序式模型)：就是一種簡單的模型，單一輸入、單一輸出，按順序一層(Dense)一層的由上往下執行。
2. Functional API：支援多個輸入、多個輸出，如 https://machinelearningmastery.com/keras-functional-api-deep-learning/ ，如下圖。

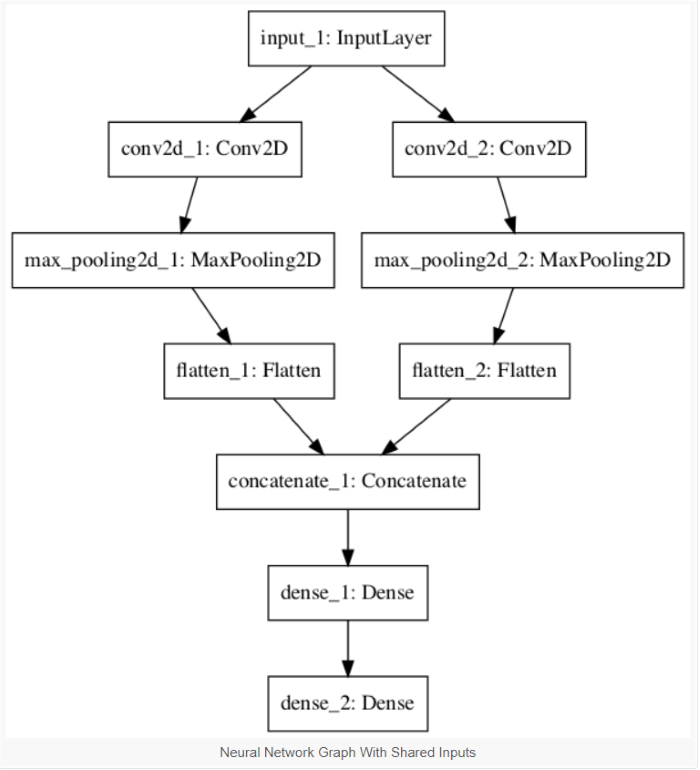
圖. Functional API 範例之流程圖

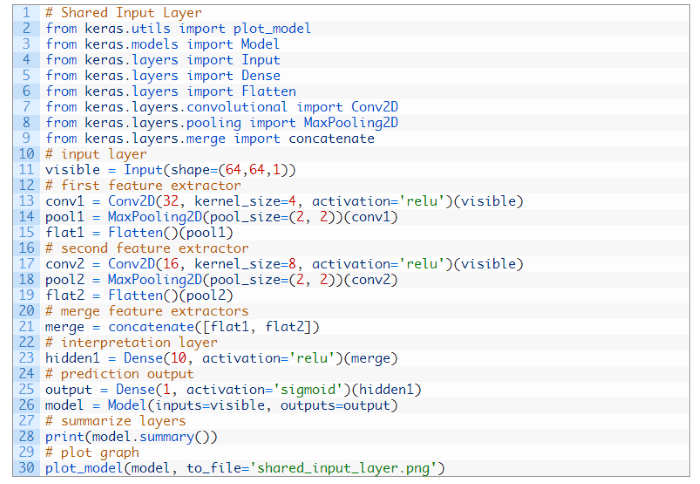
圖. Functional API 範例程式碼

後面章節 RNN/LSTM 會使用到 Functional API ，屆時再來作深入探討。

Keras 損失函數

選擇模型類別後，我們就要針對要解決的問題，決定要最小化甚麼目標函數，即損失函數(loss function)，常用的損失函數如下：

1. 均方誤差(mean_squared_error)：就是我們之前講的最小平方法(Least Square) 的目標函數 -- 預測值與實際值的差距之平均值。還有其他變形的函數, 如 mean_absolute_error、mean_absolute_percentage_error、mean_squared_logarithmic_error。
   

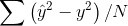
2. Hinge Error (hinge)：是一種單邊誤差，不考慮負值，適用於『支援向量機』(SVM)的最大間隔分類法(maximum-margin classification)，詳細請參考 https://en.wikipedia.org/wiki/Hinge_loss。同樣也有多種變形，squared_hinge、categorical_hinge 。
   

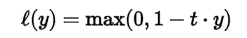
3. Cross Entropy (categorical_crossentropy)：當預測值與實際值愈相近，損失函數就愈小，反之差距很大，就會更影響損失函數的值，這篇文章 主張要用 Cross Entropy 取代 MSE，因為，在梯度下時，Cross Entropy 計算速度較快，其他變形包括 sparse_categorical_crossentropy、binary_crossentropy。
   

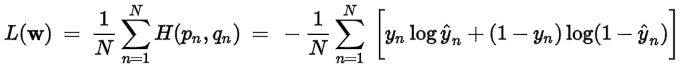
4. 其他還有 logcosh、kullback_leibler_divergence、poisson、cosine_proximity 等。

5. 注意! 損失函數、Activation Function 不限使用現成的函數，也可以自訂函數，尤其是損失函數，我們常需要自訂，例如目標函數為庫存成本，我們通常要最小化，但是，如果我們應用在銷售系統上，要極大化銷貨利益，假設庫存短缺造成無法接單，所減少的收益(L1)是兩倍於庫存的儲藏成本(L2)，損失函數就應該訂為 L1 * 2 + L2。另外，我們的目標可能是『最大化』收益，而非最小化損失，我們就必須對變數作一些轉換，使函數變為『最小化"負"收益』，因為，Keras優化都是『最小化』(Minimize)求解，沒有最大化(Maximize)。後續介紹『風格轉換』(Style Transfer)，將照片轉成不同畫風的程式，就是一個典型的例子，它為畫風(Style)定義了一個特殊的函數。

Activation Functions

Activation Function 除了提供非線性函數的轉換外，也是一種門檻(Threshold)的過濾，例如，sigmoid，將預測值(W * X) 轉為 [0,1] 之間，只有預測值大於0，才會傳導至下一層的神經元。Keras 還提供非常多種的 Activation Function，以下只列出常用的函數，其他請參考官方文件：

1. softmax：值介於 [0,1] 之間，且機率總和等於 1，適合多分類使用。
   

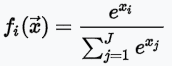
2. sigmoid：值介於 [0,1] 之間，且分布兩極化，大部分不是 0，就是 1，適合二分法。
   
   

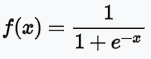
3. Relu (Rectified Linear Units)：忽略負值，介於 [0,∞] 之間。
   

4. tanh：與sigmoid類似，但值介於[-1,1]之間，即傳導有負值。
   
   

優化函數(Optimizer)

1. 隨機梯度下降法(Stochastic Gradient Descent, SGD)：就是利用偏微分，逐步按著下降的方向，尋找最佳解。它含以下參數：

   • Learning Rate (lr)：逼近最佳解的學習速率，速率訂的太小，計算最佳解的時間花費較長，訂的太大，可能會在最佳解兩旁擺盪，找不到最佳解。
   • momentum：更新的動能，一開始學習速率可以大一點，接近最佳解時，學習速率步幅就要小一點，一般訂為0.5，不要那麼大時，可改為 0.9。
   • decay：每次更新後，學習速率隨之衰減的比率。
   • nesterov：是否使用 Nesterov momentum，請參考 http://blog.csdn.net/luo123n/article/details/48239963。

2. Adam：一般而言，比SGD模型訓練成本較低，請參考『Adam - A Method for Stochastic Optimization』，包含相關參數建議值，含以下參數：

   • lr：逼近最佳解的學習速率，預設值為0.001。
   • beta_1：一階矩估計的指數衰減因子，預設值為0.9。
   • beta_2：二階矩估計的指數衰減因子，預設值為0.999。
   • epsilon：為一大於但接近 0 的數，放在分母，避免產生除以 0 的錯誤，預設值為1e-08。
   • decay：每次更新後，學習速率隨之衰減的比率。

3. 其他優化函數請參考官方文件。
   
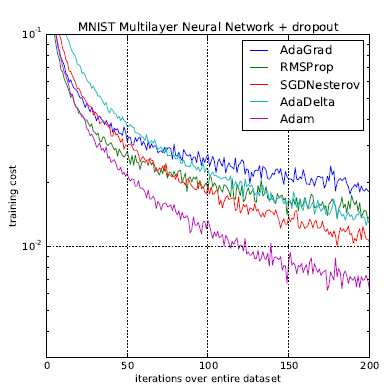
   圖. 優化函數(Optimizer)訓練成本比, 圖片來源：Adam - A Method for Stochastic Optimization

權重的初始值(kernel_initializer)

優化的程序是逐步逼近最佳解，一開始我們會選擇一個點開始，此點即稱為『權重的初始值』(kernel_initializer)，初始值的選擇可能會影響優化的結果，Keras 提供下列幾種，我們可以依問題的類型則依使用：

1. Zeros：全部為0的矩陣。
2. Ones：全部為1的矩陣。
3. Constant：全部為固定常數的矩陣。
4. Identity：對角線為 1 的矩陣。
5. RandomNormal：採常態分配的隨機亂數。
6. TruncatedNormal：裁掉極端值常態分配的隨機亂數，參數為N倍標準差。
7. RandomUniform：採均勻分配(區間內每一點機率都相同)的隨機亂數，在設定的區間內隨機抽樣。
8. 其他請參見 官方文件。

核心層(Core Layer)

以上函數為訂定問題目標，之後我們就可以在模型上加上處理方法，可包含多個不同形式的『隱藏層』(Hidden Layer)，Keras稱為『核心層』(Core Layer)，構成完整的模型。

Keras 提供的Layer包括：全連階層(Dense)、Activation layer、Dropout、Flatten、Reshape、Permute、RepeatVector、Lambda、ActivityRegularization、Masking。我們目前只使用到全連階層(Dense)，它的運算就是 output = activation(dot(input, kernel) + bias)，即前面提到的 y = g(x * W + b)。輸入的參數包括：
- units: 輸出矩陣的維數，愈大表示分類更細，擬合度愈高，雖然準確率提高，但也要防止過度擬合(Overfit)。
- activation: 使用的 Activation function，若未設定，即簡化為 y = x * W + b。
- use_bias: 是否使用偏差項(Bias)，若未設定或為 False，即簡化為 y = g(x * W)。
- kernel_initializer: 權重(W)的初始值，參見前面說明。
- bias_initializer: 偏差項(Bias)的初始值，參見前面說明。
- kernel_regularizer: 權重(W)正規化(或稱 正則項)函數，作用是對權重矩陣加上懲罰性函數(Penalty)，以防止過度擬合(overfit)，參見 regularizer。
- bias_regularizer: 偏差項(Bias)的正規化函數。
- activity_regularizer: 輸出(y)的正規化函數。
- kernel_constraint: 針對權重(W)加上限制條件，參見 constraints。
- bias_constraint: 針對偏差項(Bias)加上限制條件，參見 constraints。

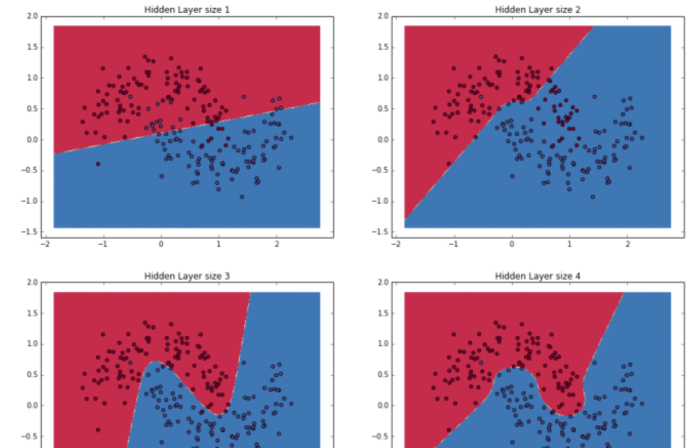
圖. 當Units變大時，分類的界線越細緻，擬合的程度越大。圖片來源：Implementing a Neural Network from Scratch in Python – An Introduction

所謂『過度擬合(overfit)』，是指使用訓練集比測試集的準確率高很多，也就是說訓練模型無法適用於預測新(未知的)資料，例如，我們在分析貸款人是否會違約，若以身分證號為X變數時，則訓練準確率將可達100%，因為一個人只有一個身分證號，但在預測新資料時，訓練資料內並無此客戶的貸款違約資料，所以，就無從判斷。碰者種狀況到，要如何解決呢? 如下圖，假設加了θ3跟θ4變數之後出現過度擬合的問題，我們就可以對θ3跟θ4乘上一個很大的數目，即懲罰性函數(Panalty)，這樣我們在最小化損失函數時，就會想辦法讓θ3跟θ4變得很小，亦即影響力趨近於0，這就是正規化(正則項, regularizer)的作法，詳細說明請參見 Machine Learning學習日記。

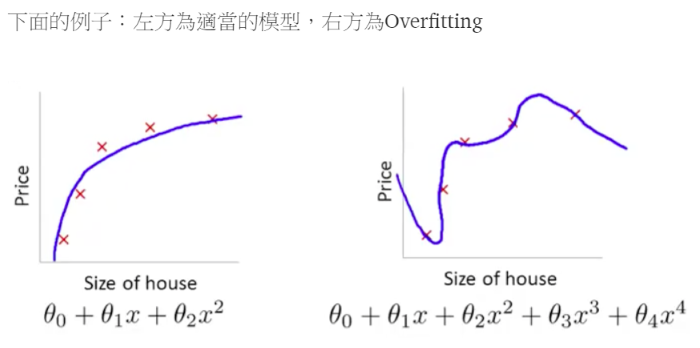
圖. 右邊加了θ3跟θ4之後出現過度擬合的問題，圖片來源：Machine Learning學習日記

結論

看完這些函數介紹，對Neural Network的運作有一個比較清楚的輪廓，如果讀者還想更徹底的了解運算法，不想使用 Keras 現成的函數，可以參考『Implementing a Neural Network from Scratch in Python – An Introduction』，它單純使用 Python 實現 Neural Network，沒有使用任何框架。

下一篇開始，我們就要開始介紹其他的演算法了，CNN登場，進行更複雜的圖形辨識及應用。