進一步理解『梯度下降』(Gradient Descent)

2018-04-01 置頂文章

梯度下降(Gradient Descent)

前言

在 Neural Network 的求解過程中，最重要而難懂的觀念應該是『梯度下降』(Gradient Descent)吧，我雖然在Day 03：Neural Network 的概念探討引用了一個比喻如下，但是，當時我的腦中還是充滿OOXX，經過一段時間思考後，總算從相關資料得到一些心得，希望與同好分享，其中也牽涉一些數學證明，如果筆者解釋不清楚，歡迎同好不吝指教。

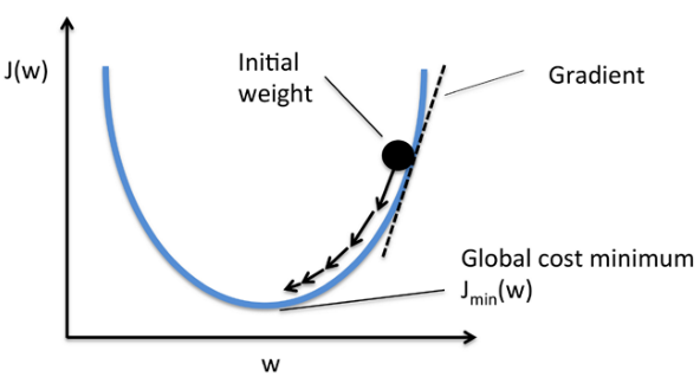
梯度下降法就好比『我們在山頂，但不知道要下山的路，於是，我們就沿路找向下坡度最大的叉路走，直到下到平地為止』。要找到向下坡度最大，在數學上常使用『偏微分』(Partial Differential)，求取斜率，一步步的逼近，直到沒有顯著改善為止，這時我們就認為是最佳解了，過程可參考下圖說明。

圖一. 梯度下降法(Gradient descent)，圖片來源：Batch gradient descent vs Stochastic gradient descent

圖解

Neural Network 的處理過程如下：

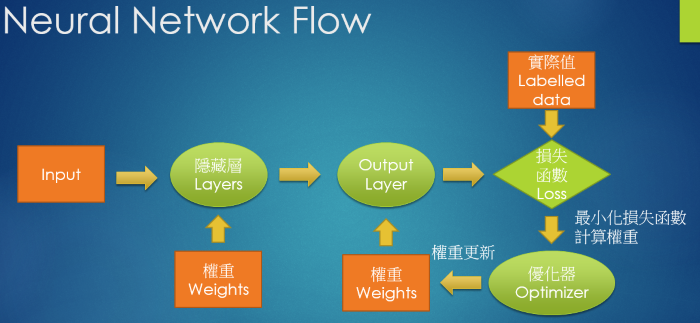
依據上圖，我們先建構好模型，決定要做幾層的隱藏層，接著，Neural Network 就會利用 Forward Propagation 及 Backpropagation 機制，如下圖，幫我們求算模型中最重要的參數 -- 『權重』(Weight)，這個過程就稱為『最佳化』(Optimization)，最常用的技巧就是『梯度下降』(Gradient Descent)。

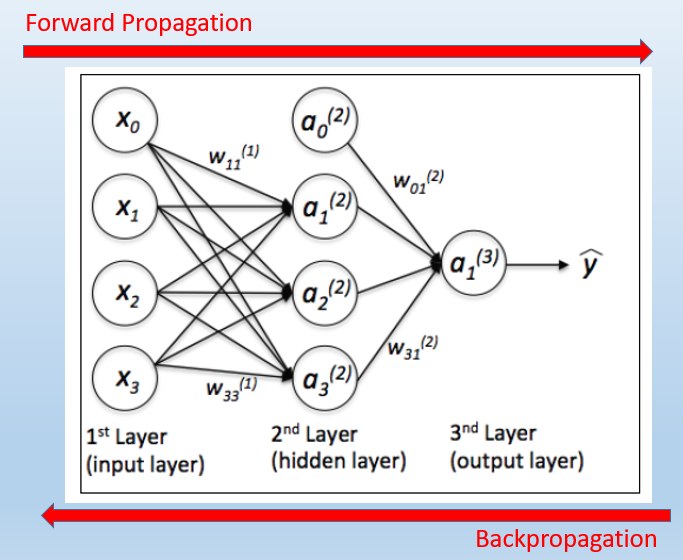
圖片來源：Python Machine Learning, Packt

接著，我們就來用圖說故事，這部份主要參考 DataCamp Deep Learning in Python 的投影片，先假設一個簡單模型如下圖，只有一層隱藏層，兩個 Input 變數值。

先任意假設一組權重(W)，如圖中紅圈內數字。
每一層的 output 就等於前一層的 input 乘以權重(W)，即 y = sum(w * x)，這個過程就是 Forward Propagation。舉例來說，隱藏層的第一個節點(Node)就等於 2 * 1 + 3 * 1 = 5, 第二個節點就等於 2 * -1 + 3 * 1 = 1，output層就等於 5 * 2 + 1 * -1 = 9。

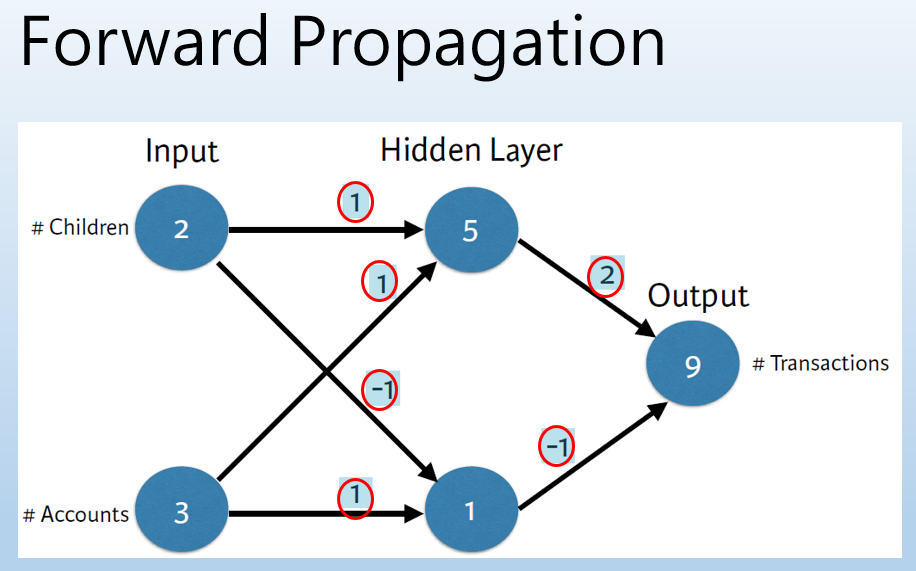
圖片來源：DataCamp Deep Learning in Python

接著，我們就反推回去(Backpropagation)，用『梯度下降法』，逐步調整權重(W)，慢慢逼近最佳解，以達到『損失函數最小化』。如圖一，我們先求算梯度(Gradient)，再依梯度往下走，損失就會越來越小，梯度的公式等於 -2 * input * (y實際值 - y 預測值)，後續會證明。再接續上圖，假設已知資料的ouput實際值為 13，那損失就等於 13-9 = 4，這時的output對隱藏層兩個節點的梯度就分別等於 -2 * 5 * 4 = -40 及 -2 * 1 * 4 = -8，因此，我們，就可以設定下降的步幅，即學習率(Learning Rate)，譬如 0.01，所以，調整新權重 = 原權重 - (學習率 * 梯度)，推算出所有的權重後，再回到步驟2，不斷循環，直到損失的縮小已經不顯著了，我們就認定那一組權重是最佳解了。公式整理如下：

梯度數學證明

先以上例說明，梯度可以使用『最小平方估計法』(Ordinary Least Sequare, OLS)求得，利用偏微分求『梯度』，如下圖。

如果有 bias：即 y = b + w * x，只要等式兩邊各減 b，變成 y' = w * x，還是可以用上圖推導，公式不變。
通常會看到 SSE 會乘上 ½，書上說是為了計算方便。

範例程式

參考『梯度下降法快速教程 _ 第一章：Python简易实现以及对学习率的探讨 - CSDN博客』，整理如下，程式名稱為 gd1.py：

import numpy as np
import matplotlib.pyplot as plt

# 目標函數:y=x^2
def func(x): return np.square(x)

# 目標函數一階導數:dy/dx=2*x
def dfunc(x): return 2 * x

def GD(x_start, df, epochs, lr):    
    """  梯度下降法。給定起始點與目標函數的一階導函數，求在epochs次反覆運算中x的更新值
        :param x_start: x的起始點    
        :param df: 目標函數的一階導函數    
        :param epochs: 反覆運算週期    
        :param lr: 學習率    
        :return: x在每次反覆運算後的位置（包括起始點），長度為epochs+1    
     """    
    xs = np.zeros(epochs+1)    
    x = x_start    
    xs[0] = x    
    for i in range(epochs):         
        dx = df(x)        
        # v表示x要改變的幅度        
        v = - dx * lr        
        x += v        
        xs[i+1] = x    
    return xs

# Main
# 起始權重
x_start = 5    
# 執行週期數
epochs = 15 
# 學習率   
lr = 0.3   
# 梯度下降法 
x = GD(x_start, dfunc, epochs, lr=lr) 
print (x)
# 輸出：[-5.     -2.     -0.8    -0.32   -0.128  -0.0512]

color = 'r'    
#plt.plot(line_x, line_y, c='b')    
from numpy import arange
t = arange(-6.0, 6.0, 0.01)
plt.plot(t, func(t), c='b')
plt.plot(x, func(x), c=color, label='lr={}'.format(lr))    
plt.scatter(x, func(x), c=color, )    
plt.legend()

plt.show()

方式執行： python gd1.py
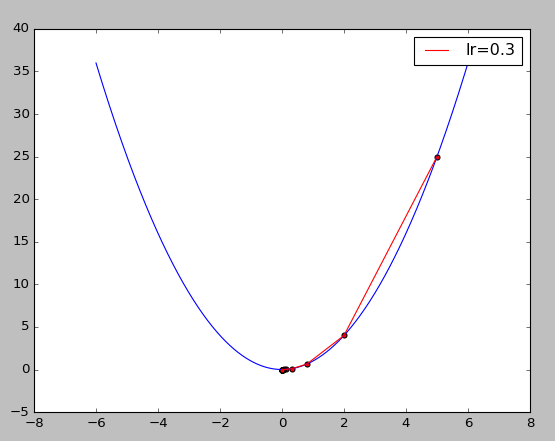
結果如下圖，藍色曲線是損失函數或目標函數，紅色折線是以『梯度下降法』逼近最佳解的過程(由上而下)。
dfunc 是 func 偏微分的公式，X^2 偏微分等於 2 * X，讀者可以同時改變 func、dfunc 內容，試試看結果是否依然正確。
調整其它 Hyperparameters，例如 x_start、epochs、lr，測試逼近的過程。
學習率(lr) 設的過大就會像下圖右，左右跳動，可能求不到最佳解。

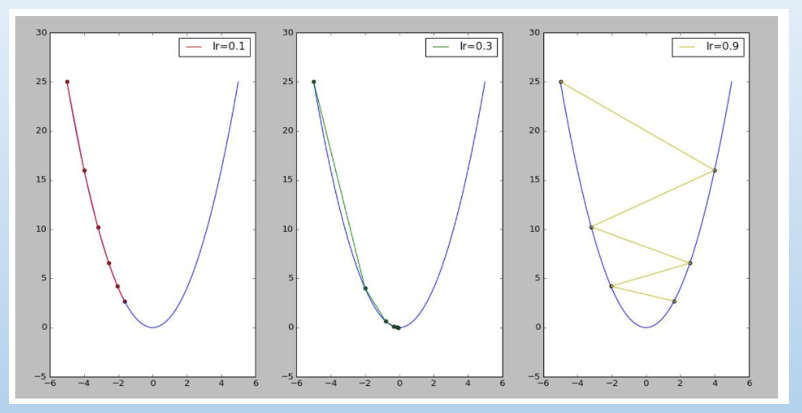
圖片來源：『梯度下降法快速教程 _ 第一章：Python简易实现以及对学习率的探讨 - CSDN博客』

結語

經過鐵人賽連續30天的自我凌虐後，休養生息，發現功力還是在小學程度，決定打掉重練，把每個環節搞清楚，希望有朝一日能打通任督二脈，歡迎讀者能隨時加持一下。

回首頁

Code Bank

輕鬆寫程式，簡單過生活 ~~~