一般我們在做研究的時候總有些數據是需要被分析的,尤其是那種並非線性成長的數據,因為這種數據對研究人員來說其實是很頭痛的且很難用人工的方法所計算出數據的趨勢與最小差,有鑑於此我們可以透過對數趨勢線來幫助研究人員得知數據的規則以及參考的價值。
本篇文章將引導您學會使用對數趨勢線來觀看數據的趨勢分布。
一般我們在做研究的時候總有些數據是需要被分析的,尤其是那種並非線性成長的數據,因為這種數據對研究人員來說其實是很頭痛的且很難用人工的方法所計算出數據的趨勢與最小差,有鑑於此我們可以透過對數趨勢線來幫助研究人員得知數據的規則以及參考的價值。
本篇文章將引導您學會使用對數趨勢線來觀看數據的趨勢分布。
對數趨勢線主要是適合用在一開始數據變化很大,到後期變化輛緩和的數據分布。
那也因為我們在測量數據的時候並不是使用類比的方始來測量,而使是用數位的方式來測量,
也就是說我們並不是持續不間斷地在蒐集資料,而是區段性的在收集資料,那在每一個區段間的數據我們應該如何來補差呢?
也就是我們在這篇文章要探討的議題,可以透過對數趨勢線來幫助研究人員進行補差的運算,
而這個運算的背後並不是你我可以在短時間了解的複雜數學公式,那這個功能呢已經內建在Excel當中了。
現在正是進入議題,假設我們要分析的是車子在不同時間點的速度效能。
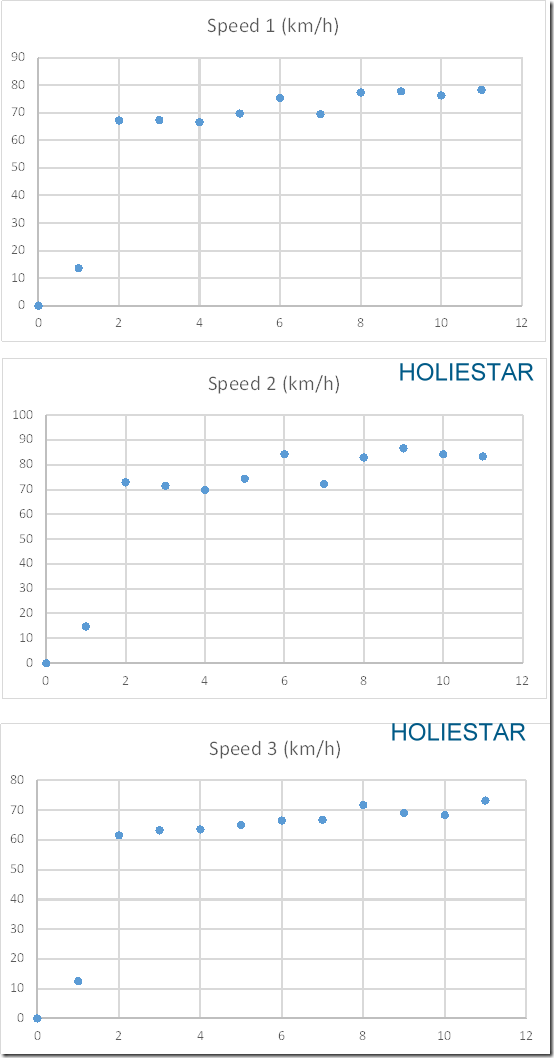
我們分別測試了三次,分別為Speed1、Speed2、Speed3 在不同秒數下所測的移動速度(時速),並且建立了下表:
在表中的秒數0的部分是輸入了1E-12代表的是10的負12次方,
為什麼要這樣做呢?其實是因為在後面我們要用到的對數趨勢線沒有辦法在數據中有0的時候使用
(表中資訊為假資料,請不要問為什麼車子突然減速,這只是舉例)
| Time (S) | 1E-12 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Speed 1 (km/h) | 1E-12 | 14 | 67 | 67 | 67 | 70 | 75 | 69 | 77 | 78 | 76 | 78 |
| Speed 2 (km/h) | 1E-12 | 15 | 73 | 72 | 70 | 74 | 84 | 72 | 83 | 87 | 84 | 83 |
| Speed 3 (km/h) | 1E-12 | 13 | 62 | 63 | 64 | 65 | 66 | 67 | 72 | 69 | 68 | 73 |
那表只是資料,我們必須將表轉換回有用的資訊,
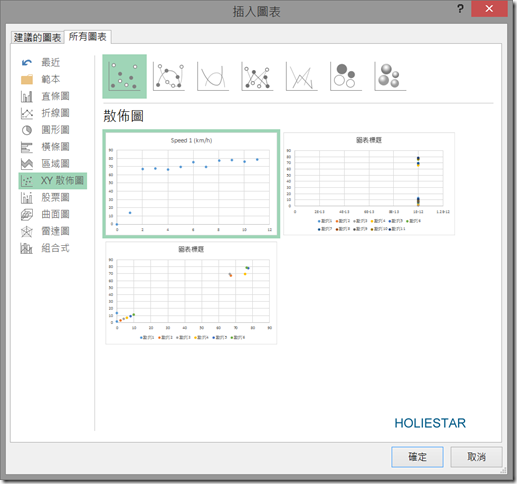
透過插入圖表,選擇XY散佈圖
就會自動建立圖表了,並且可以看到車子移動速度在不同秒數上的分布囉!!
那假設想要取得在1.5秒時車子的移動速度應該如何取?!
使用1秒的速度加上2秒的速度除以2嗎? 錯 ! !
我們一開始就說了 這是一個非線性的資料數據,所以不可以使用線性的方式來自動補差,
這時候對數趨勢線就派上用場了
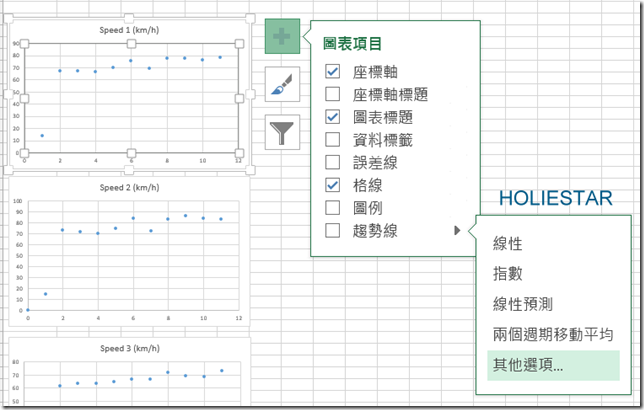
點選在圖表旁邊的【+】→【趨勢線】→【其他選項】
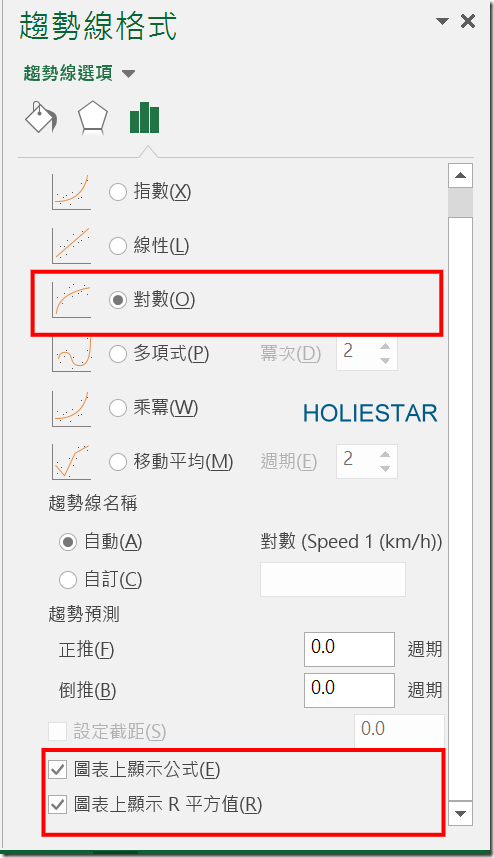
勾選【對數】,並且將【公式】與【R平方】顯示出來
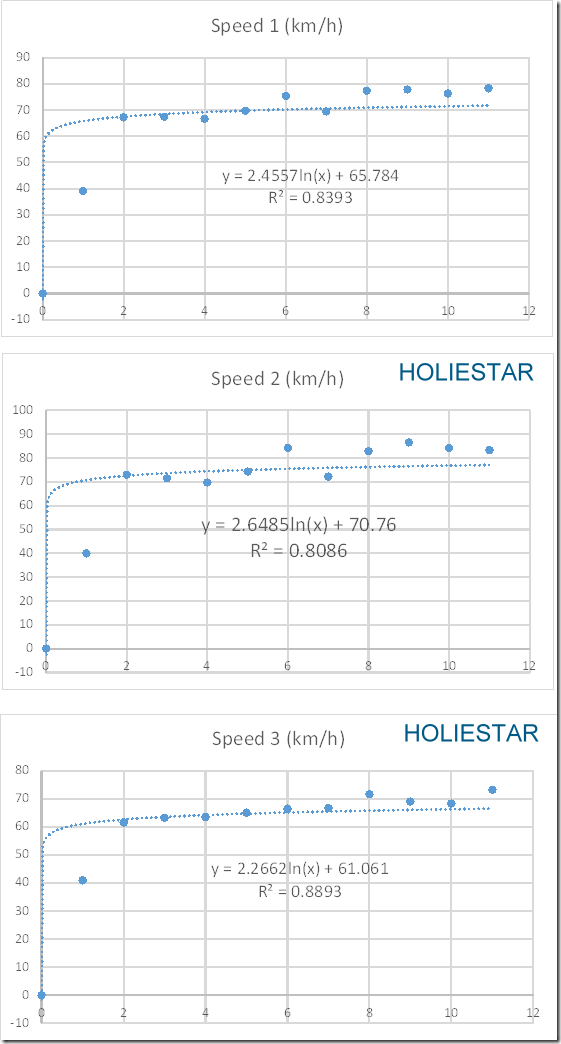
如此重複三次 我們可以得知三次的測量分析圖表
那在圖表中的R平方式代表著這個數據的可用性,它的範圍為0~1,若越接近1則該數據的可用性較高,比較適合用於後續的研究參考
若較低的話則代表著該次測量的數據分布也不是對數可以分析出其相關性,也表示著該數據其實是不是和用來做後續研究參考的
那剛剛說到要取得1.5秒時的移動速度應該如何來算,以Speed1為例Excel已經幫我們寫好公式了也就是 y = 2.4557ln(x) + 65.784
此時我們的X軸是秒數只要將X帶入1.5就可以知道在1.5秒鐘車子移動的速度了,使用對數的方式來補差會比線性的補差方式還要來的精準,
並且背後是有理論在支持的在撰寫論文上相對審稿教授就比較不會針對這個不分刁難你了!!
如此以來我們便學會了使用對數趨勢線來觀看數據的趨勢分布
References : http://office.microsoft.com/zh-tw/help/HP005262321.aspx
文章中的敘述如有觀念不正確錯誤的部分,歡迎告知指正 謝謝
轉載請註明出處,並且附上本篇文章網址 ! 感謝。