雜記:利用Excel 計算T分數
最近因為接了一個任務要利用Excel計算某項測驗中考生的T分數。
此次任務交接得到先前的檔案資料在T分數計算的公式為 =
50+10*STANDARDIZE(K2,AVERAGE($K$2:$K$20),STDEV($K$2:$K$20))
為了確認此公式無誤，把以前學過的教育統計書又拿出來對照一下：
這個Excel計算T分數公式使用了三個Excel函式
STANDARDIZE
AVERAGE
STDEV
查了Excel的線上說明關於STANDARDIZE(標準化)這個函數的說明
STANDARDIZE(x, mean, standard_dev)
STANDARDIZE 函數語法具有下列引數：
· X 必要。 這是要標準化的值。
· Mean 必要。這是分配的算術平均值。
· Standard_dev 必要。這是分配的標準差。
註解
· 如果 standard_dev ≤ 0，STANDARDIZE 會傳回 #NUM! 錯誤值。
· 將數值標準化的方程式為：
![clip_image001[4]](https://dotblogsfile.blob.core.windows.net/user/yangmoore/1508/Excel-T_7B0C/clip_image001%5B4%5D.gif "clip_image001[4]"){kind=small}
從上述說明可知在T分數計算公式中STANDARDIZE的參數中也用到AVERAGE(平均)與STDEV(標準差)，所以這個公式和書本上的公式T=50+10Z 是一樣的。
在我負責的任務上，確認公式無誤後，其實只需要把考生的成績正確輸入，再套入以上T分數的計算公式，把成績算出來即可。
不過在處理任務的過程中，我比較有興趣的是為什麼單一考場用原始分數，多考場則用T分數來決定錄取人，因為這讓我想起20多年前的事。
話說從前，第1次聽到T分數這個名詞，是從寢室的大四學長口中聽到的，學長說：『決定師大畢業生分發順序的依據就是比較每個學生學業成績的T分數，因為當時有三所師範學校相同科系要一起分發，因為各校的評分標準不同所以採用T分數來評比。』
雖然分發這樣重要的事是依據T分數高低，但是說實在我直到分發完了，也搞不清楚T分數如何計算，為什麼要用T分數而不是用各校自己的排名？雖然在教育統計學上有介紹，但是自己並不想去了解，其中原因是一方面自己成績太爛，不管用什麼分數去算大概都難逃發配邊疆，再者深受馬克吐溫的說法影響：謊言有三種；謊言、可惡的謊言及統計。阿Q的想法既然統計是謊言，幹嘛花時間去了解一個謊言。
但是這次事關別人的前途，不想良心不安，才把以前封箱的教育統計書又拿出來，仔細的研究一下。
首先什麼是T分數？T分數是『標準分數』的一種，常見的『標準分數』除了Z分數、T分數之外，還有離差智商。所謂的『標準分數』是把個別原始分數與整體平均分數的差距轉換以『標準差』為單位計算後的值，再進行不同線性轉換即可得到的不同的標準分數，而只轉換為標準差單位而未進行線性轉換的分數即所謂的Z分數，依照上述舉例說明Z分數的計算：
假設某考生的分數為 X
該考場的所有考生的平均分數為 Xav
該考場的所有考生分數的標準差為 STD
則Z分數: Z=(X-Xav)/STD
從上式可以看出來Z分數就是算個別原始分數與平均分數的差相當於幾個標準差，這樣的轉換可以把不同群體原始分數絕對高低差異轉換成相對幾個標準差單位，這樣不同的群體可以進行比較客觀的比較，但是這有一個假設前題，即這不同群體必須是常態分佈(Normal Distribution) (後面再來討論)。
Z分數這樣的算法，當個別原始分數小於平均分數時Z分數為負值，這樣的資料呈現上對於一般人容易造成誤解，所以通常不會直接使用Z分數，而是將Z分數再進行線性轉換。
例如T分數是Z分數進行線性轉換的分數
T=50+10*Z
所以不同考場有不同的評分者，為了消除評分者原始絕對分數高低差，所以採取T分數進行評比。
有的老師問我：為什麼有的教師甄選採用的T分數算法是T=70+10*Z ？
其實只要大家在那場甄試所使用的線性轉換方式都一致，並不影響個別之間成績的高低比較，反正是挑相對高T分者錄取，加70或加50代表的只是：我們要指定原始分數剛好是平均分數者，其轉換的T分數是50分或70分。
像現在常用的智力測驗的成績也是進行標準化再線性轉換的結果，早期的智力測驗指的是採用了比率智商，此智商是將心理年齡與生理年齡的比值乘以100，現在以離差智商取代。
比西智力測驗的離差智商＝16Z＋100
(比西智力測驗的平均數100，標準差16)
魏氏智力測驗的離差智商＝15Z＋100
(魏氏智力測驗的平均數100，標準差15)
回到前述不管是那一種標準分數，其前題假設是母群體是常態分配 。
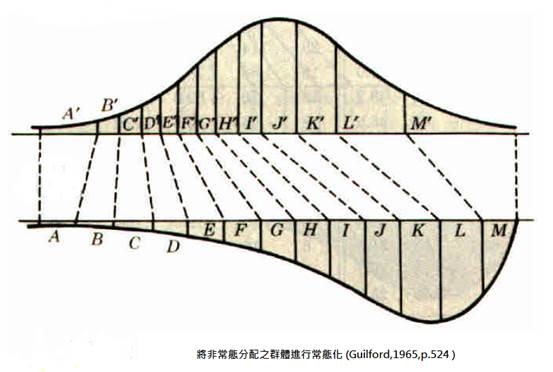
如果兩個母群體不是常態分配，這樣使用標準分數來評比兩群體中個體的成績高低容易失真，所以如果母群體不是常態分配，為了修正失真的情況，會採取一些修正措施將原始分數轉換為符合常態分配的標準分數, 此種分數稱為常態化標準分數。
說到這裡有基本一個問題，這些標準分數的設計是使用統計學的概念去發展，在母群體數量太少下，這樣的計分方式是否客觀，也許只能銷彌部分評審主觀的評分因素。
常態累積機率表(Cumulative normal distribution probability tables)
|
ｚ |
0 |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.06 |
0.07 |
0.08 |
0.09 |
|
0 |
0.5 |
0.504 |
0.508 |
0.512 |
0.516 |
0.5199 |
0.5239 |
0.5279 |
0.5319 |
0.5359 |
|
0.1 |
0.5398 |
0.5438 |
0.5478 |
0.5517 |
0.5557 |
0.5596 |
0.5636 |
0.5675 |
0.5714 |
0.5753 |
|
0.2 |
0.5793 |
0.5832 |
0.5871 |
0.591 |
0.5948 |
0.5987 |
0.6026 |
0.6064 |
0.6103 |
0.6141 |
|
0.3 |
0.6179 |
0.6217 |
0.6255 |
0.6293 |
0.6331 |
0.6368 |
0.6406 |
0.6443 |
0.648 |
0.6517 |
|
0.4 |
0.6554 |
0.6591 |
0.6628 |
0.6664 |
0.67 |
0.6736 |
0.6772 |
0.6808 |
0.6844 |
0.6879 |
|
0.5 |
0.6915 |
0.695 |
0.6985 |
0.7019 |
0.7054 |
0.7088 |
0.7123 |
0.7157 |
0.719 |
0.7224 |
|
0.6 |
0.7257 |
0.7291 |
0.7324 |
0.7357 |
0.7389 |
0.7422 |
0.7454 |
0.7486 |
0.7517 |
0.7549 |
|
0.7 |
0.758 |
0.7611 |
0.7642 |
0.7673 |
0.7704 |
0.7734 |
0.7764 |
0.7794 |
0.7823 |
0.7852 |
|
0.8 |
0.7881 |
0.791 |
0.7939 |
0.7967 |
0.7995 |
0.8023 |
0.8051 |
0.8078 |
0.8106 |
0.8133 |
|
0.9 |
0.8159 |
0.8186 |
0.8212 |
0.8238 |
0.8264 |
0.8289 |
0.8315 |
0.834 |
0.8365 |
0.8389 |
|
1 |
0.8413 |
0.8438 |
0.8461 |
0.8485 |
0.8508 |
0.8531 |
0.8554 |
0.8577 |
0.8599 |
0.8621 |
|
1.1 |
0.8643 |
0.8665 |
0.8686 |
0.8708 |
0.8729 |
0.8749 |
0.877 |
0.879 |
0.881 |
0.883 |
|
1.2 |
0.8849 |
0.8869 |
0.8888 |
0.8907 |
0.8925 |
0.8944 |
0.8962 |
0.898 |
0.8997 |
0.9015 |
|
1.3 |
0.9032 |
0.9049 |
0.9066 |
0.9082 |
0.9099 |
0.9115 |
0.9131 |
0.9147 |
0.9162 |
0.9177 |
|
1.4 |
0.9192 |
0.9207 |
0.9222 |
0.9236 |
0.9251 |
0.9265 |
0.9279 |
0.9292 |
0.9306 |
0.9319 |
|
1.5 |
0.9332 |
0.9345 |
0.9357 |
0.937 |
0.9382 |
0.9394 |
0.9406 |
0.9418 |
0.9429 |
0.9441 |
|
1.6 |
0.9452 |
0.9463 |
0.9474 |
0.9484 |
0.9495 |
0.9505 |
0.9515 |
0.9525 |
0.9535 |
0.9545 |
|
1.7 |
0.9554 |
0.9564 |
0.9573 |
0.9582 |
0.9591 |
0.9599 |
0.9608 |
0.9616 |
0.9625 |
0.9633 |
|
1.8 |
0.9641 |
0.9649 |
0.9656 |
0.9664 |
0.9671 |
0.9678 |
0.9686 |
0.9693 |
0.9699 |
0.9706 |
|
1.9 |
0.9713 |
0.9719 |
0.9726 |
0.9732 |
0.9738 |
0.9744 |
0.975 |
0.9756 |
0.9761 |
0.9767 |
|
2 |
0.9772 |
0.9778 |
0.9783 |
0.9788 |
0.9793 |
0.9798 |
0.9803 |
0.9808 |
0.9812 |
0.9817 |
|
2.1 |
0.9821 |
0.9826 |
0.983 |
0.9834 |
0.9838 |
0.9842 |
0.9846 |
0.985 |
0.9854 |
0.9857 |
|
2.2 |
0.9861 |
0.9864 |
0.9868 |
0.9871 |
0.9875 |
0.9878 |
0.9881 |
0.9884 |
0.9887 |
0.989 |
|
2.3 |
0.9893 |
0.9896 |
0.9898 |
0.9901 |
0.9904 |
0.9906 |
0.9909 |
0.9911 |
0.9913 |
0.9916 |
|
2.4 |
0.9918 |
0.992 |
0.9922 |
0.9925 |
0.9927 |
0.9929 |
0.9931 |
0.9932 |
0.9934 |
0.9936 |
|
2.5 |
0.9938 |
0.994 |
0.9941 |
0.9943 |
0.9945 |
0.9946 |
0.9948 |
0.9949 |
0.9951 |
0.9952 |
|
2.6 |
0.9953 |
0.9955 |
0.9956 |
0.9957 |
0.9959 |
0.996 |
0.9961 |
0.9962 |
0.9963 |
0.9964 |
|
2.7 |
0.9965 |
0.9966 |
0.9967 |
0.9968 |
0.9969 |
0.997 |
0.9971 |
0.9972 |
0.9973 |
0.9974 |
|
2.8 |
0.9974 |
0.9975 |
0.9976 |
0.9977 |
0.9977 |
0.9978 |
0.9979 |
0.9979 |
0.998 |
0.9981 |
|
2.9 |
0.9981 |
0.9982 |
0.9982 |
0.9983 |
0.9984 |
0.9984 |
0.9985 |
0.9985 |
0.9986 |
0.9986 |
|
3 |
0.9987 |
0.9987 |
0.9987 |
0.9988 |
0.9988 |
0.9989 |
0.9989 |
0.9989 |
0.999 |
0.999 |
|
3.1 |
0.999 |
0.9991 |
0.9991 |
0.9991 |
0.9992 |
0.9992 |
0.9992 |
0.9992 |
0.9993 |
0.9993 |
|
3.2 |
0.9993 |
0.9993 |
0.9994 |
0.9994 |
0.9994 |
0.9994 |
0.9994 |
0.9995 |
0.9995 |
0.9995 |
|
3.3 |
0.9995 |
0.9995 |
0.9995 |
0.9996 |
0.9996 |
0.9996 |
0.9996 |
0.9996 |
0.9996 |
0.9997 |
|
3.4 |
0.9997 |
0.9997 |
0.9997 |
0.9997 |
0.9997 |
0.9997 |
0.9997 |
0.9997 |
0.9997 |
0.9998 |
歡迎引用，請注明來源出處!