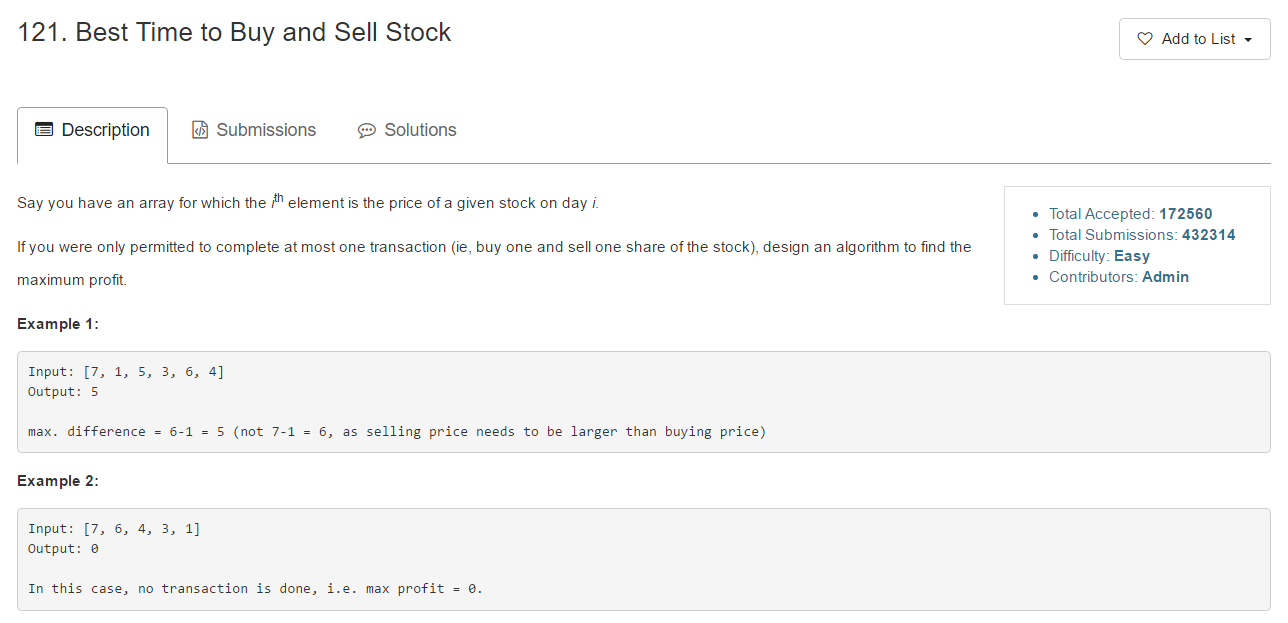
Step 1: 新增一個測試案例,prices 長度為 2,no transaction done。
【測試代碼】prices 為 {5,4}, 因為怎麼買賣都不會賺錢,所以 max profit 為 0。

【生產代碼】
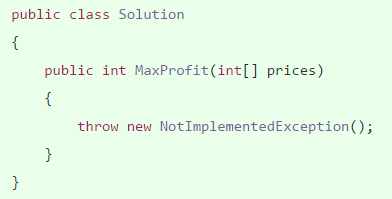
Step 2: hard-code 判斷前者比後者大,則回傳0。
【生產代碼】如果 prices[1] 比 prices[0] 小,回傳 0。

【重構測試代碼】擷取方法,將 assertion 行為抽取到 AssertMaxProfitShouldBe()
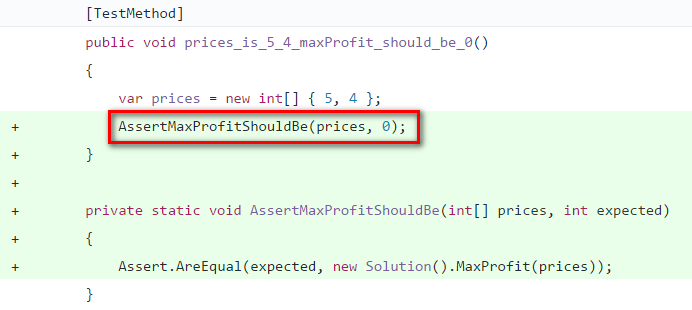
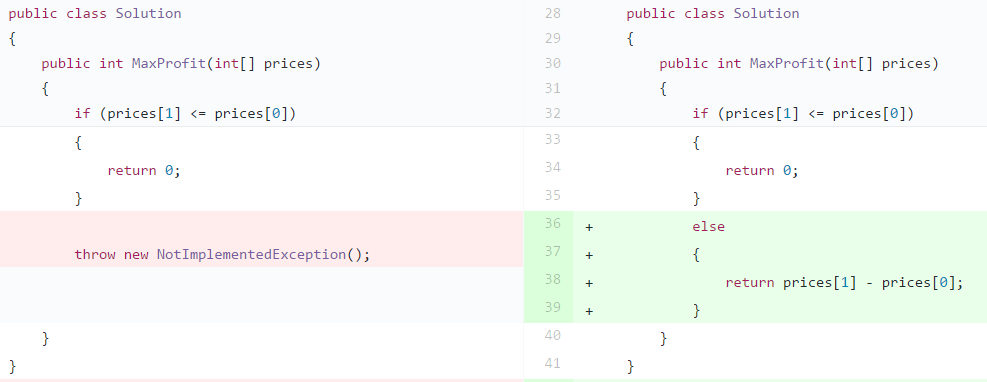
Step 3: 新增測試案例,prices 長度仍為 2,後者比較大,回傳差值。
【測試代碼】

【生產代碼】hard-code 判斷當後者比前者大時,回傳兩者差值,即為 max profit。
Step 4: 新增測試案例,prices 長度為 3, 最大值為最後一位。
【測試代碼】預期會失敗,因為期望結果為 3,目前實現的生產代碼實際結果為 2。強制驅動生產代碼設計,當數字長度不只 2 位時,該怎麼處理。

【生產代碼】透過 Skip(1) 取得剩下的 prices, 並且取其中最大值,與目前比較的 price 取差值。(仍屬 hard-code 階段)
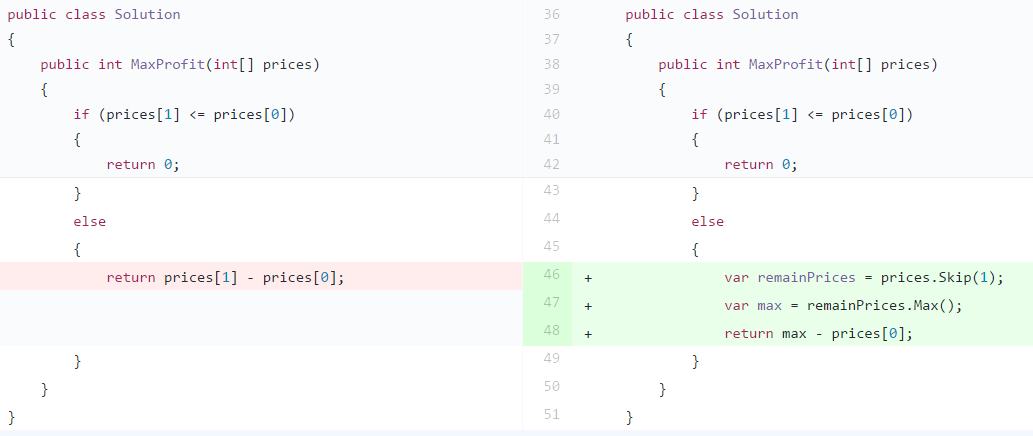
Step 5: 新增通過的測試案例
【新增預期通過的測試代碼】prices 為 {4,7,6} 也可以符合 remainPrices 與取 Max() 差值的需求。因為比較點仍在 prices[0] 的 4。

【新增預期通過的測試代碼】即使 prices 長度不只是 3, 只要 prices[0] 是比較值,目前的生產代碼就能滿足此需求。

Step 6: 新增測試案例,prices[1] < prices[0],prices 長度為 3
【測試代碼】強制驅動生產代碼的第一個 if block 進行修改,擺脫 hard-code prices[1] 的部分。因為原本生產代碼的實現會回傳 0,但這個測試案例預期回傳為 6,所以會驗證失敗。

【生產代碼】類似 Step 4 的方式處理,只是 flag 改成 prices[1]。
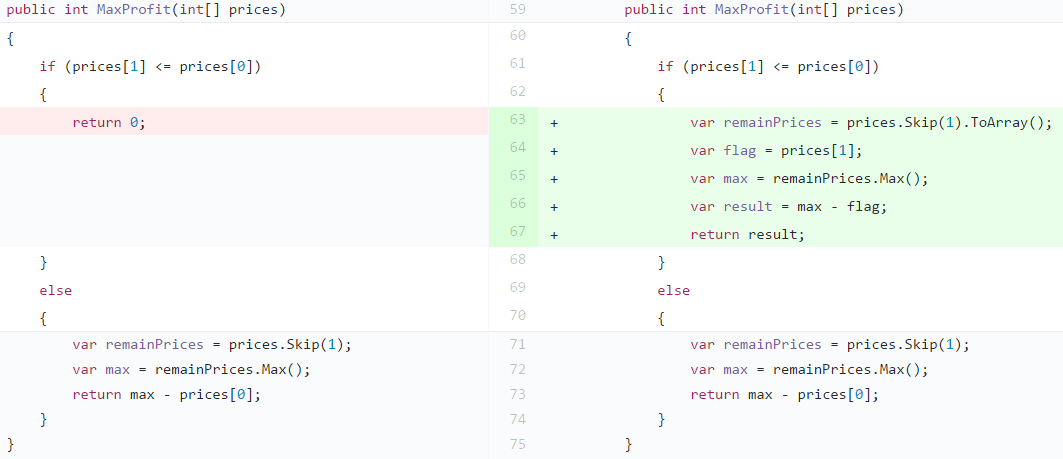
【重構】將 if/else block 中,duplicate 的部分抽取到 if/else block 之外。
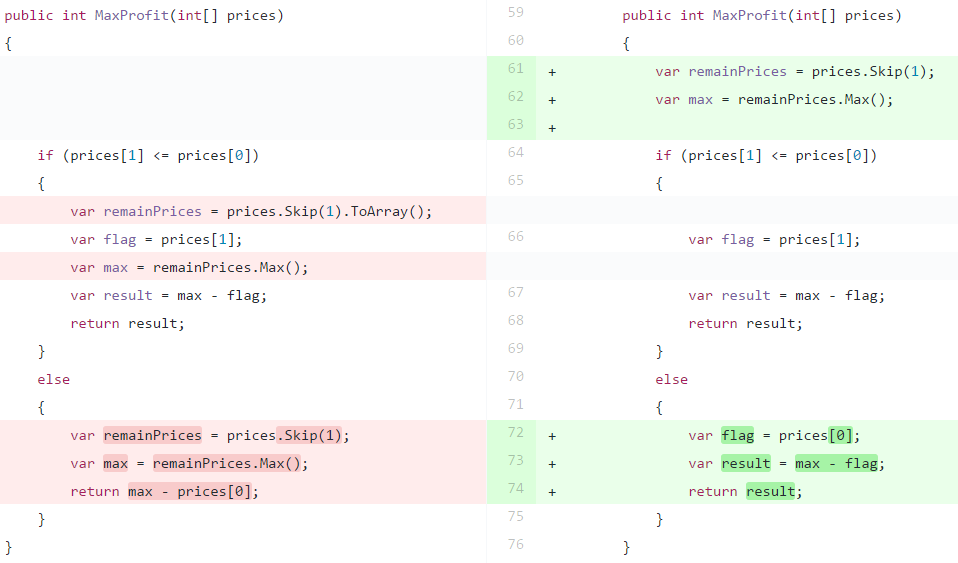
Step 7: 重構 algorithm, 改成遞迴處理
【生產代碼】每一個 price 都跟剩餘的 prices[] 中的最大值做差值,保留最大差值即為 max profit。
public class Solution
{
public int MaxProfit(int[] prices)
{
return FindMaxProfitFromNextPrice(prices[0], prices.Skip(1), 0);
}
private int FindMaxProfitFromNextPrice(int flag, IEnumerable<int> remainPrices, int lastMaxProfit)
{
if (!remainPrices.Any())
{
return lastMaxProfit;
}
var max = remainPrices.Max();
var currentMaxProfit = max - flag;
var maxProfit = Math.Max(lastMaxProfit, currentMaxProfit);
return FindMaxProfitFromNextPrice(remainPrices.ElementAt(0), remainPrices.Skip(1), maxProfit);
}
}
到目前為止,需求所需商業邏輯已經完整實現,但很遺憾的,無法通過 LeetCode 上效能的測試案例。
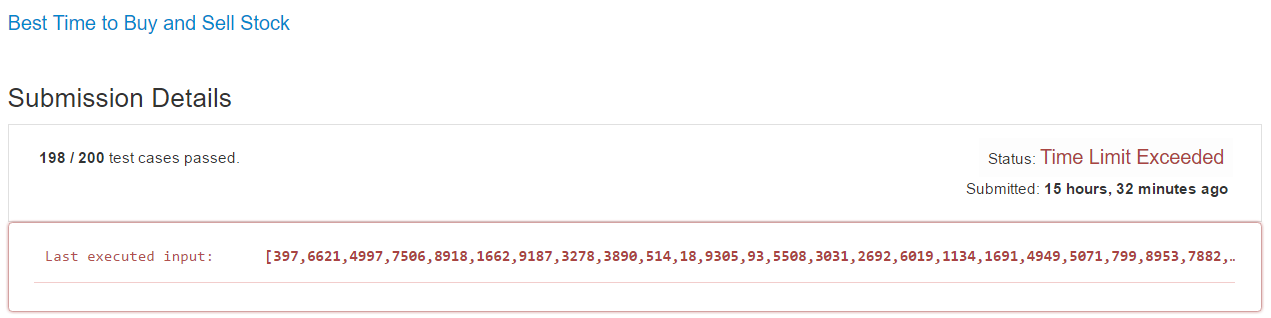
Step 8: Kadane's algorithm 的實現
【生產代碼】Kadane's algorithm 說明:
- 一串數列的最大差值,其實是差值的總和(這邊的
currentSum),直到滿足第二點的條件,代表數列結束。例如:{4,6,7} 最大差值的7 - 4 = 3, 可以被轉成(6-4) + (7-6) = 3 - 當
currentSum < 0時,代表截至目前為止,這一段最大總和已決定。所以要 reset 為 0, 以便計算下一段的最大差值。 maxSum用來存放每一段的最大差值。
public class Solution
{
public int MaxProfit(int[] prices)
{
if (prices.Length < 2)
{
return 0;
}
return FindMaxProfitByKadane(prices);
}
private int FindMaxProfitByKadane(int[] prices)
{
var currentSum = 0;
var maxSum = 0;
for (int i = 1; i < prices.Length; i++)
{
currentSum = Math.Max(0, currentSum += prices[i] - prices[i - 1]); //less than 0, reset to 0
maxSum = Math.Max(maxSum, currentSum);
}
return maxSum;
}
}
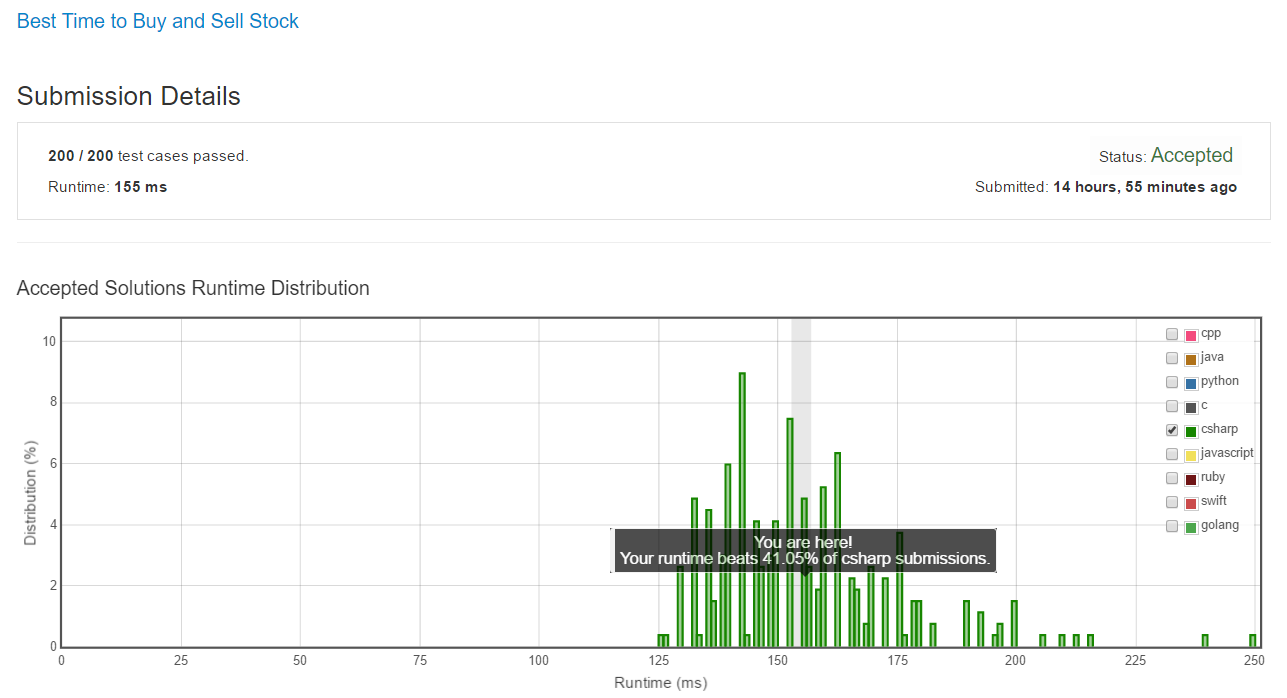
通過 LeetCode 上所有測試案例
結論
練習這一題 LeetCode ,我的心路歷程:
- 有趣的題目,有感,看起來有點難又不會太難
- TDD 一下練手感
- 抽象,淬取出遞迴的方式
- 絞盡腦汁,碰到無法突破的效能瓶頸
- 上網找相關解法,瞭解到針對這特殊需求的處理方式。原來這樣的需求用這樣的 algorithm 是可以巧妙解決的。多開的地圖包含:Maximum subarray problem, Kadane's algorithm, 動態規劃,其實現方式、原理與使用場景。
說真的,這一題如果拿來當面試考題,我覺得可以寫出「易讀且可滿足完整需求」的虛擬碼就剛好了,Kadane's algorithm 的解法當交朋友閒聊或題目補充就夠了。
blog 與課程更新內容,請前往新站位置:http://tdd.best/
